Comparing two unpaired means#
Introduction#
In hypothesis testing, the unpaired t-test is a valuable tool for determining if two separate groups have truly different average values. Whether we’re investigating the impact of a new drug on blood pressure or comparing crop yields from two different fertilizers, the unpaired t-test helps us draw statistically sound conclusions from our data.
We use the unpaired t-test specifically when we have two independent groups or samples. These groups are not paired or matched in any way. For instance, we might have one group of patients receiving a new medication and another group receiving a placebo. The test assesses whether any observed difference in the means of these two groups is statistically significant or simply due to chance.
Before applying the unpaired t-test, it’s important to make sure our data meets certain assumptions:
Independence: the observations within each group should be independent of each other.
Normality: the data within each group should ideally follow a normal distribution. However, the t-test is reasonably robust to moderate deviations from normality, especially with larger sample sizes.
Equal variances: the variances of the two groups should be approximately equal. If the variances differ significantly, alternative versions of the t-test (such as Welch’s t-test) can be used.
The unpaired t-test works by calculating a test statistic that quantifies the difference between the means of the two groups relative to the variability within each group. This test statistic follows a known distribution (the t-distribution) under the null hypothesis of no difference between the group means. By comparing the calculated test statistic to the expected distribution, we obtain a P value. If the P value falls below our chosen significance level (alpha), we reject the null hypothesis and conclude that a statistically significant difference exists between the two group means.
In the following sections, we’ll delve deeper into the mathematical foundations of the unpaired t-test, explore its practical applications, and provide the knowledge needed to confidently apply this test in our own analyses.
Preparing data for hypothesis testing#
Descriptive statistics and visualization#
In this section, we will introduce the importance of descriptive statistics and visualization in understanding the characteristics of the two samples being compared. We will emphasize how these techniques provide valuable insights into the central tendency, spread, and distribution of the data, which are crucial for interpreting the results of the unpaired t-test.
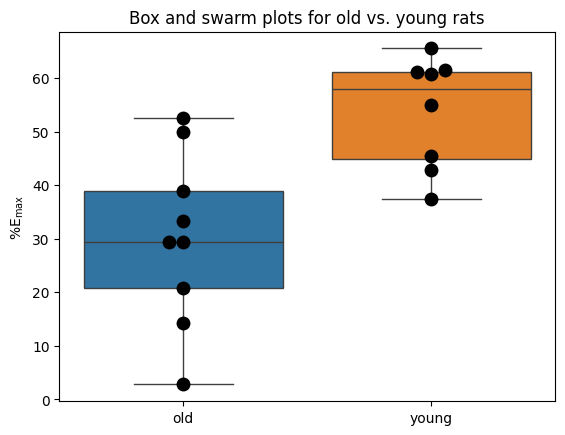
Frazier and colleagues investigated the impact of norepinephrine on bladder muscle relaxation in rats. Their study specifically examined the maximum relaxation (\(\%\text{E}_\text{max}\)) achievable with high doses of this neurotransmitter, comparing the responses of old (‘old’) and young (‘yng’) rats.
import numpy as np
# We use the data from Table 30.1 of the book Intuitive Biostatistics
old = np.array([20.8, 2.8, 50, 33.3, 29.4, 38.9, 29.4, 52.6, 14.3]) # old rats
yng = np.array([45.5, 55, 60.7, 61.5, 61.1, 65.5, 42.9, 37.5]) # young rats
import scipy.stats as stats
# Descriptive statistics
old_stats = stats.describe(old)
yng_stats = stats.describe(yng)
print("Descriptive statistics for 'old':\n", old_stats, '\n')
print("Descriptive statistics for 'young':\n", yng_stats)
Descriptive statistics for 'old':
DescribeResult(nobs=9, minmax=(2.8, 52.6), mean=30.16666666666667, variance=259.0375, skewness=-0.17569385392311104, kurtosis=-0.8080848898945967)
Descriptive statistics for 'young':
DescribeResult(nobs=8, minmax=(37.5, 65.5), mean=53.7125, variance=107.4069642857143, skewness=-0.4421628669270582, kurtosis=-1.3632352105713499)
import matplotlib.pyplot as plt
import seaborn as sns
# Box and swarm plots
sns.boxplot(data=[old, yng])
sns.swarmplot(data=[old, yng], color='black', size=10)
plt.ylabel(r"$\%\text{E}_\text{max}$")
plt.xticks([0, 1], ['old', 'young'])
plt.title("Box and swarm plots for old vs. young rats");
Assessing assumptions#
Before proceeding with any hypothesis test, it’s crucial to verify that our data adheres to the underlying assumptions of the chosen statistical method. This subsection emphasizes the importance of checking for normality and homogeneity of variance, two common assumptions in many parametric tests, including the unpaired t-test. We’ll briefly discuss the methods used to assess these assumptions, such as normality tests and tests for equal variances, and outline the potential consequences of violating these assumptions. Additionally, we’ll highlight the available remedies or alternative approaches when assumptions are not met, ensuring the robustness and validity of our statistical inferences.
Normality testing#
One of the fundamental assumptions of the unpaired t-test is that the data within each group is approximately normally distributed. To assess this assumption, we employ normality tests such as the D’Agostino-Pearson omnibus K² and Shapiro-Wilk tests, or visual inspections of histograms or Q-Q plots, as discussed in greater details in a previous chapter about normality test. These tests help us gauge whether the observed data aligns with the expected characteristics of a normal distribution.
# Normality tests
# D'Agostino-Pearson K² test
k2_old, pval_k2_old = stats.normaltest(old)
k2_yng, pval_k2_yng = stats.normaltest(yng)
print(
'old',
f"D'Agostino-Pearson omnibus: K2={k2_old:.2f}, P value={pval_k2_old:.3f}",
sep='\t')
print(
'young',
f"D'Agostino-Pearson omnibus: K2={k2_yng:.2f}, P value={pval_k2_yng:.3f}",
sep='\t')
# Shapiro-Wilk
shapiro_old, pval_shapiro_old = stats.shapiro(old)
shapiro_yng, pval_shapiro_yng = stats.shapiro(yng)
print(
'old',
f"Shapiro-Wilk's normality test P value={pval_shapiro_old:.3f}",
sep='\t')
print(
'young',
f"Shapiro-Wilk's normality test P value={pval_shapiro_yng:.3f}",
sep='\t')
# Interpret the results
alpha = 0.05 # Set the desired significance level
if (pval_k2_old > alpha and pval_k2_yng > alpha) \
or (pval_shapiro_old > alpha and pval_shapiro_yng > alpha):
print("\nBoth groups' data are not inconsistent with a normal distribution\n\
(failed to reject null hypothesis of normality)")
else:
print("\nAt least one group's data is not consistent with a normal distribution")
old D'Agostino-Pearson omnibus: K2=0.11, P value=0.947
young D'Agostino-Pearson omnibus: K2=1.75, P value=0.418
old Shapiro-Wilk's normality test P value=0.900
young Shapiro-Wilk's normality test P value=0.238
Both groups' data are not inconsistent with a normal distribution
(failed to reject null hypothesis of normality)
c:\Users\Sébastien\Documents\data_science\biostatistics\intuitive_biostatistics\.env\Lib\site-packages\scipy\stats\_axis_nan_policy.py:418: UserWarning: `kurtosistest` p-value may be inaccurate with fewer than 20 observations; only n=9 observations were given.
return hypotest_fun_in(*args, **kwds)
c:\Users\Sébastien\Documents\data_science\biostatistics\intuitive_biostatistics\.env\Lib\site-packages\scipy\stats\_axis_nan_policy.py:418: UserWarning: `kurtosistest` p-value may be inaccurate with fewer than 20 observations; only n=8 observations were given.
return hypotest_fun_in(*args, **kwds)
Pingouin’s normality function actually performs both the Shapiro-Wilk test and the D’Agostino-Pearson test.
import pingouin as pg
# Function to perform tests and print results
def normality_tests(data, sample_type):
s = f"{'Test':<20} {'W':<6} {'P value':<8} {'normal'}"
print(f"Normality tests for {sample_type}".center(len(s), "-"))
print(s)
# D'Agostino-Pearson Test
dagostino_results = pg.normality(data, method='normaltest')
print(f"{'D\'Agostino-Pearson':<20} {dagostino_results['W'][0]:<6.2f} \
{dagostino_results['pval'][0]:<8.3f} {dagostino_results['normal'][0]}")
# Shapiro-Wilk Test
shapiro_results = pg.normality(
data,
method='shapiro')
print(f"{'Shapiro-Wilk':<20} {shapiro_results['W'][0]:<6.2f} \
{shapiro_results['pval'][0]:<8.3f} {shapiro_results['normal'][0]}")
print("-" * len(s))
# Perform tests and print results
normality_tests(old, "old rats")
print('\n')
normality_tests(yng, "young rats")
--------Normality tests for old rats-------
Test W P value normal
D'Agostino-Pearson 0.11 0.947 True
Shapiro-Wilk 0.97 0.900 True
-------------------------------------------
-------Normality tests for young rats------
Test W P value normal
D'Agostino-Pearson 1.75 0.418 True
Shapiro-Wilk 0.89 0.238 True
-------------------------------------------
c:\Users\Sébastien\Documents\data_science\biostatistics\intuitive_biostatistics\.env\Lib\site-packages\scipy\stats\_axis_nan_policy.py:418: UserWarning: `kurtosistest` p-value may be inaccurate with fewer than 20 observations; only n=8 observations were given.
return hypotest_fun_in(*args, **kwds)
Additionally, the Pingouin library provides a convenient function for generating Q-Q plots, which offer a visual assessment of normality by comparing the observed data quantiles against the expected quantiles of a normal distribution.
# Plotting Q-Q plots
fig, axes = plt.subplots(1, 2)
titles = ["Q-Q plot: old rats", "Q-Q plot: young rats"]
for i, (data, title) in enumerate(zip([old, yng], titles)):
pg.qqplot(
data,
dist='norm',
ax=axes[i],
confidence=0.95,)
axes[i].set_title(title)
plt.tight_layout() # Ensures plots don't overlap
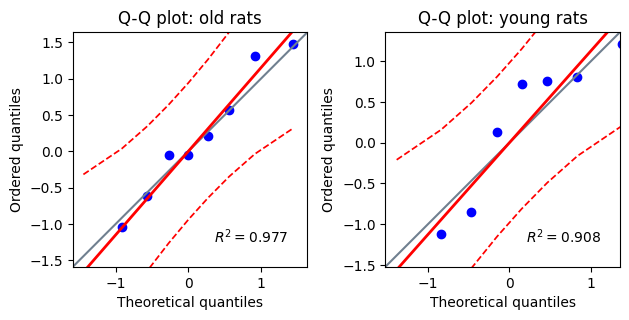
While the unpaired t-test is reasonably robust to moderate deviations from normality, especially with larger sample sizes, severe violations can impact the accuracy of the test’s results. When the normality assumption is not met, the calculated P value may be unreliable, potentially leading to incorrect conclusions about the statistical significance of the difference between group means.
In such cases, we have a few options:
Transform the data: if the data exhibits a clear pattern of non-normality, we might attempt to transform it (e.g., using log transformations or square root transformations) to achieve a more normal distribution.
Use non-parametric alternatives: when transformations are ineffective or impractical, we can consider non-parametric tests like the Mann-Whitney U test, as discussed in the dedicated section, which do not rely on the normality assumption.
Proceed with caution: if the sample sizes are relatively large and the deviations from normality are not severe, we might proceed with the unpaired t-test, acknowledging the potential limitations in the interpretation of the results.
Homoscedasticity testing#
Another crucial assumption underlying the unpaired t-test is that the variances (or spreads) of the two groups being compared are approximately equal. This property is known as homoscedasticity. In this subsection, we’ll explore the importance of this assumption and introduce statistical tests, such as Levene’s test, that help us assess whether our data meets this criterion.
F-test of equality of variances#
The F-test, formally known as the F-test of equality of variances, is a statistical method used to compare the variances of two or more groups. In our context, it assesses whether the ‘old’ and ‘young’ groups have significantly different variances. The test calculates an F-statistic based on the ratio of the group variances and their respective sample sizes. This F-statistic is then compared to an F-distribution to obtain a P value.
# Calculate sample variances s (unbiased estimator)
var_old = np.var(old, ddof=1)
var_yng = np.var(yng, ddof=1)
# Calculate the ratio of variances
var_ratio = var_old / var_yng
# Sample sizes
n_old = len(old)
n_yng = len(yng)
# Degrees of freedom
df_old = n_old - 1
df_yng = n_yng - 1
# Calculate the F-statistic
f_statistic = max(var_ratio, 1/var_ratio) # ensures that the F-statistic >= 1
# Calculate the p-value using the F-distribution (two-sided test)
p_value_fstat = 2 * (1 - stats.f.cdf(f_statistic, df_old, df_yng))
# Print the results
print(f"Variance ratio (old/young) = {var_ratio:.3f}")
print(f"F-statistic = {f_statistic:.3f}")
print(f"P value for the F-test of equal variance (manual calculation) = {p_value_fstat:.4f}")
Variance ratio (old/young) = 2.412
F-statistic = 2.412
P value for the F-test of equal variance (manual calculation) = 0.2631
Assuming the null hypothesis of equal variances is true, there is a 26.31% probability that we would observe a discrepancy between the sample standard deviations as large as (or larger than) the one we found, purely due to random sampling. Let’s visualize the F-statistic (F), critical F-value (F*), and the area (P value) under the F distribution corresponding to our dataset.
# Significance level (alpha)
α = 0.05
# Calculate critical value
f_crit = stats.f.ppf(1 - α, df_old, df_yng)
# Generate x values for plotting
x = np.linspace(0, 10, 100)
hx = stats.f.pdf(x, df_old, df_yng)
# Create the plot
plt.plot(x, hx, lw=2, color="black")
# Plot the critical value
plt.axvline(
x=f_crit, # type: ignore
color='orangered',
linestyle='--',
label=f'F* ({f_crit:.3f})')
# Shade the probability alpha
plt.fill_between(
x[x >= f_crit],
hx[x >= f_crit],
linestyle="-",
linewidth=2,
color='tomato',
label=f'α ({α})')
# Plot the observed F-statistic
plt.axvline(
x=f_statistic, # type: ignore
color='limegreen',
linestyle='-.',
label=f'F ({f_statistic:.3f})')
# Shade the P value area
plt.fill_between(
x[x >= f_statistic],
hx[x >= f_statistic],
color='greenyellow',
label=f'P ({p_value_fstat:.3f})')
# Add labels and title
plt.xlabel('F')
plt.ylabel('Density')
plt.margins(x=0.05, y=0)
plt.yticks([])
plt.title(f"F-distribution (DFn={df_old}, DFd={df_yng})")
plt.legend();
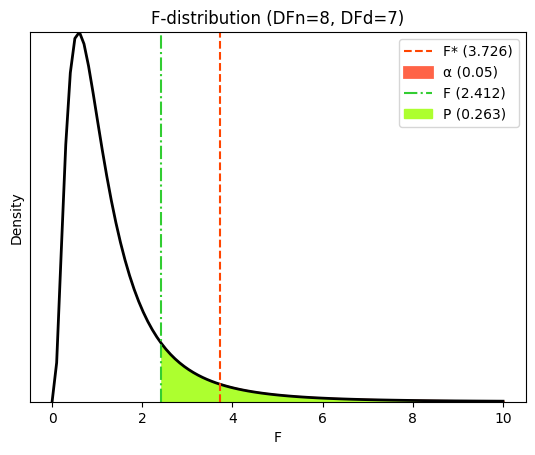
In the context of homoscedasticity tests like Levene’s test or Bartlett’s test, the null hypothesis states that the variances are equal.
Therefore:
High P value: we fail to reject the null hypothesis, meaning we do not have enough evidence to say the variances are different. This suggests that the assumption of equal variances is reasonable.
Low P value: we reject the null hypothesis, meaning we have evidence to suggest the variances are not equal. This indicates that the assumption of equal variances is violated.
Levene and Bartlett tests#
We’ll now leverage the convenience and robustness of Levene’s and Bartlett’s tests to evaluate the assumption of equal variances. A deeper dive into the manual F-statistic calculation will come later when we cover ANOVA.
Levene’s test assesses the equality of variances across groups by analyzing the spread of the absolute deviations from a central measure (typically the median) within each group. The test statistic calculated in Levene’s test approximately follows an F-distribution under the null hypothesis of equal variances. This allows us to compute a P value to determine the statistical significance of any observed differences in variances.
Bartlett’s test also evaluates the homogeneity of variances across groups, but it operates under the assumption that the data within each group is normally distributed. The test statistic in Bartlett’s test approximately follows a chi-squared distribution with degrees of freedom equal to the number of groups minus one, again enabling us to obtain a P value for hypothesis testing.
While both tests serve the same purpose, Levene’s test is generally considered more robust to deviations from normality compared to Bartlett’s test. Therefore, if we suspect or have evidence that the data might not be perfectly normally distributed, Levene’s test is often the preferred choice. On the other hand, if we’re confident about the normality of the data, Bartlett’s test can be a suitable option.
# Using scipy.stats
# Levene's test for equal variances
levene_statistic, levene_p_value = stats.levene(old, yng)
# Bartlett's test for equal variances
bartlett_statistic, bartlett_p_value = stats.bartlett(old, yng)
# Print the results
print(f"Levene's test statistic = {levene_statistic:.3f}, \
P value = {levene_p_value:.4f}")
print(f"Bartlett's test statistic = {bartlett_statistic:.3f}, \
P value = {bartlett_p_value:.4f}")
Levene's test statistic = 0.686, P value = 0.4204
Bartlett's test statistic = 1.290, P value = 0.2560
# Using pingouin
# Levene's test for equal variances
levene_results = pg.homoscedasticity([old, yng], method='levene')
# Bartlett's test for equal variances
bartlett_results = pg.homoscedasticity([old, yng], method='bartlett')
# Print the results
print("Levene and Bartlett's test results:")
print(levene_results)
print(bartlett_results)
Levene and Bartlett's test results:
W pval equal_var
levene 0.686405 0.420378 True
T pval equal_var
bartlett 1.290011 0.256046 True
A small P value, indicating a potential violation of the equal variances assumption, presents a nuanced situation. While some fields, including certain areas of biology, might tolerate minor deviations from homoscedasticity, it’s generally advisable to adopt a more conservative approach. Consider using Welch’s t-test, which is designed to handle unequal variances, or explore data transformations that might improve the homogeneity of variances. In cases of severe non-normality or highly unequal variances, especially with small sample sizes, consider using the non-parametric Mann-Whitney U test as a robust alternative to Welch’s t-test, or a bootstrap approach, both discussed at the end of this chapter.
Assessing the significance of mean differences with t-test#
The central question in many research studies is whether an intervention, treatment, or characteristic leads to a meaningful difference between groups. In this section, we’ll explore how the unpaired t-test helps us answer this question by comparing the means of two independent samples.
mean_diff = np.mean(yng) - np.mean(old)
print(f"Mean difference between old and young rats = {mean_diff:.3f}")
Mean difference between old and young rats = 23.546
The t-ratio#
At the core of the unpaired t-test lies the t-ratio, also named t-value, or t-score, and abbreviated t, a pivotal statistic that quantifies the disparity between the means of two groups relative to their combined variability. The t-ratio used in the unpaired t-test shares a structural resemblance to the t-statistic we encountered earlier when constructing confidence intervals for a single mean in a previous chapter. Both involve a ratio of a difference to a measure of variability and follow a t-distribution. However, the t-ratio in the unpaired t-test focuses on comparing two sample means, while the t-statistic for confidence intervals is used to estimate a single population mean.
In this subsection, we’ll delve into the mathematical underpinnings of the t-ratio, exploring how it incorporates sample means, variances, and sample sizes to provide a standardized measure of the difference between groups. Understanding the t-ratio is crucial for interpreting the results of the unpaired t-test and drawing meaningful conclusions about the statistical significance of any observed differences.
Welch’s t-test#
Manual calculation of the Welch’s t-ratio#
In the general case, where we do not assume equal variances, the t-ratio for the unpaired t-test is often referred to as Welch’s t-statistic. This test utilizes the following t-statistic:
where \(\bar x_1\) and \(\bar x_2\) are the sample means, \(s_1^2\) and \(s_2^2\) are the sample variances of the two groups, and \(n_1\) and \(n_2\) are the sample sizes. Remember the relationships between variance \(s^2\), standard deviation \(s\), and standard error of the mean: \(s_{\overline{x}} = s / \sqrt{n}\).
The standard error of the difference between the means with “unequal variances”, denoted by \(s_{\bar x_1 - \bar x_2}\), is calculated as the square root of the sum of the estimated variances of the two sample means:
This standard error accounts for the variability within each group and is used in the denominator of Welch’s t-statistic:
The degrees of freedom for this t-statistic are approximated using the Welch-Satterthwaite equation, which can be further simplified using standard errors:
# Calculate the standard error for unequal variances (Welch's t-test)
# The variances were already calculated for the F-test
se_unequal = np.sqrt(var_old / n_old + var_yng / n_yng)
# Calculate Welch's t-statistic
t_statistic_welch = mean_diff / se_unequal
# Calculate the degrees of freedom using the Welch-Satterthwaite equation
df_welch = se_unequal**4 / ((var_old/n_old)**2/(n_old-1) + (var_yng/n_yng)**2/(n_yng-1))
# se^2 = s/n --> se^4 = (s/n)^2
# Or using the intermediate formula
#df_welch = se_unequal**4 / (((var_old/n_old)** 2)/(n_old-1) + ((var_yng/n_yng)** 2)/(n_yng-1))
# Print the results
print(f"t-statistic (Welch's) = {t_statistic_welch:.4f} with {df_welch:.3f} \
degrees of freedom (Welch-Satterthwaite approximation)")
t-statistic (Welch's) = 3.6242 with 13.778 degrees of freedom (Welch-Satterthwaite approximation)
Welch’s P value#
Now that we have our t-statistic and degrees of freedom, we can determine the P value associated with our test. The P value will quantify the probability of observing a t-statistic as extreme as (or more extreme than) the one we calculated, assuming the null hypothesis of no difference between the group means is true. We will utilize the cumulative distribution function (CDF) of the t-distribution to compute this probability.
# Calculate the P value using the t-distribution (two-sided test)
p_value_welch = 2 * (1 - stats.t.cdf(abs(t_statistic_welch), df_welch))
# Print the results
print(f"P value for Welch's t-test = {p_value_welch:.5f}")
P value for Welch's t-test = 0.00283
Visualizing Welch’s values#
To gain a deeper understanding of the results of Welch’s t-test, let’s visualize the t-statistic, the critical t-values that define the rejection regions, and the areas under the t-distribution corresponding to the P value. This visual representation will help us grasp the statistical significance of the observed difference between the group means and the role of the degrees of freedom in shaping the t-distribution.
# Significance level (alpha)
α = 0.05
# Calculate critical t-values (two-tailed test)
t_crit_lower_welch = stats.t.ppf(α/2, df_welch)
t_crit_upper_welch = stats.t.ppf(1 - α/2, df_welch)
# Generate x values for plotting
x = np.linspace(-5, 5, 1000)
hx = stats.t.pdf(x, df_welch)
# Create the plot
plt.plot(x, hx, lw=2, color="black")
# Plot the critical t-values
plt.axvline(
x=t_crit_upper_welch, # type: ignore
color='orangered',
linestyle='--',
label=f't* ({t_crit_upper_welch:.3f})')
plt.axvline(
x=t_crit_lower_welch, # type: ignore
color='orangered',
linestyle='--',)
# Shade the rejection regions (alpha)
plt.fill_between(
x[x <= t_crit_lower_welch],
hx[x <= t_crit_lower_welch],
linestyle="-",
linewidth=2,
color='tomato',
label=f'α ({α})')
plt.fill_between(
x[x >= t_crit_upper_welch],
hx[x >= t_crit_upper_welch],
linestyle="-",
linewidth=2,
color='tomato')
# Plot the observed t-statistic
plt.axvline(
x=t_statistic_welch,
color='limegreen',
linestyle='-.',
label=f't ({t_statistic_welch:.3f})')
# Shade the P-value areas (two-tailed)
plt.fill_between(
x[x <= -abs(t_statistic_welch)],
hx[x <= -abs(t_statistic_welch)],
color='greenyellow',
label=fr'P ({p_value_welch:.3f})',)
plt.fill_between(
x[x >= abs(t_statistic_welch)],
hx[x >= abs(t_statistic_welch)],
color='greenyellow')
# Add labels and title
plt.xlabel('t')
plt.ylabel('Density')
plt.margins(x=0.05, y=0)
plt.yticks([])
plt.title(f"t-distribution (DF={df_welch:.2f}) | Welch, two-tailed")
plt.legend();
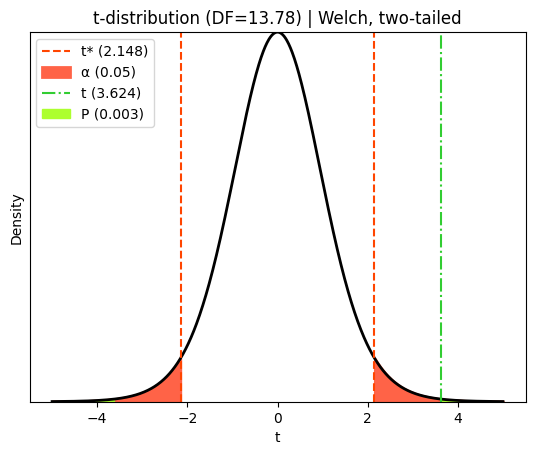
The red dashed lines in this diagram represent the critical t-values that define the rejection regions for a two-tailed t-test at a 5% significance level. The ‘tails’ of the curve outside these lines each represent 2.5% of the probability distribution under the null hypothesis (that the true population mean difference is zero).
The green dot-dashed line represents the observed t-statistic calculated from our sample data. The P value corresponds to the total probability of observing a t-statistic as extreme as (or more extreme than) the one we calculated, assuming the null hypothesis is true. In a two-tailed test like this, we consider both tails of the distribution because the true population mean difference could be either higher or lower than zero. One-tailed tests (as shown later) are used when we have a directional hypothesis, specifically testing if the difference is ‘less than zero’ or ‘greater than zero’.
Welch’s confidence interval#
A confidence interval provides a range of plausible values for the true difference in population means when comparing two unpaired groups using the Welch test. It gives us an idea of the precision of our estimate of this difference.
To calculate this confidence interval, we need to consider the variability within each group, acknowledging that these variances may not be equal. Here’s how it’s done:
Calculate the point estimate: this is the difference between the sample means of the two groups as \(\bar X_1 - \bar X_2\)
Calculate the standard error: the standard error of the difference in means for the Welch test is calculated as \(s_{\bar x_1 - \bar x_2} = \sqrt{s_1^2 / n_1 + s_2^2 / n_2}\), where \(s_1\) and \(s_2\) are the sample standard deviations of the two groups, and \(n_1\) and \(n_2\) are the respective sample sizes
Determine the degrees of freedom: the degrees of freedom for the Welch test are calculated using a rather complex formula (Welch-Satterthwaite equation) to account for the unequal variances
Find the critical t-value: using the desired confidence level (e.g., 95%) and the calculated degrees of freedom, find the corresponding critical t-value from the t-distribution table or using statistical software
Calculate the margin of error: multiply the standard error by the critical t-value: \(W = t^\ast \times s_{\bar x_1 - \bar x_2}\)
Construct the confidence interval: subtract and add the margin of error to the point estimate to obtain the lower and upper bounds of the confidence interval: \((\bar X_1 - \bar X_2) \pm W\), where \(W\) is the margin of error
# Calculate the confidence interval (e.g., 95% confidence)
confidence_level = 0.95
margin_of_error_welch = abs(stats.t.ppf((1 + confidence_level) / 2, df_welch)) * se_unequal
ci_welch = (mean_diff - margin_of_error_welch, mean_diff + margin_of_error_welch)
# Print the results
print(f"Mean difference (young - old) = {mean_diff:.3f}")
print(f"95% confidence interval for the mean difference: \
[{ci_welch[0]:.3f}, {ci_welch[1]:.3f}]")
Mean difference (young - old) = 23.546
95% confidence interval for the mean difference: [9.591, 37.501]
Performing the Welch’s t-test in Python#
Let’ts conduct Welch’s t-test using both the SciPy and Pingouin libraries in Python. We’ll compare their implementations and outputs, highlighting their respective advantages.
# Welch's t-test using SciPy
t_statistic_scipy_welch, p_value_scipy_welch = stats.ttest_ind(yng, old, equal_var=False)
# Welch's t-test using Pingouin
ttest_results_pingouin_welch = pg.ttest(yng, old, correction=True) # type: ignore
# Print the results
print("Welch's t-test results (SciPy):")
print(f"t-statistic = {t_statistic_scipy_welch:.3f}, \
P value = {p_value_scipy_welch:.4f}")
print("\nWelch's t-test results (Pingouin):")
ttest_results_pingouin_welch
Welch's t-test results (SciPy):
t-statistic = 3.624, P value = 0.0028
Welch's t-test results (Pingouin):
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 3.624246 | 13.777968 | two-sided | 0.002828 | [9.59, 37.5] | 1.715995 | 14.51 | 0.909532 |
The Welch’s t-test yielded a t-statistic of 3.624 with an associated P value of 0.003. This P value is less than the commonly used significance level of 0.05, indicating strong evidence to reject the null hypothesis of no difference between the means of the old and young groups of rats. Therefore, we conclude that there is a statistically significant difference in the \(\%\text{E}_\text{max}\) between the two groups.
Furthermore, the 95% confidence interval for the mean difference (young - old) is [9.591, 37.501]. This suggests that we can be 95% confident that the true population mean difference lies within this range. The fact that this interval does not include zero further supports the conclusion that the two groups are significantly different.
Student t-test#
While Welch’s t-test offers a robust approach for comparing means when variances might be unequal, there are scenarios where we have reason to believe that the variances of the two groups are approximately the same. In such cases, we can employ the standard unpaired t-test, also known as Student’s t-test. This test relies on the assumption of equal variances, leading to a slightly simpler formula for the t-statistic and a different calculation for the degrees of freedom.
Student’s t-ratio formula#
Starting from the general formula of the t-ratio, and under the assumption of equal variance where \(s_1^2 = s_2^2 = s_p^2\), the t-ratio for the unpaired t-test assuming equal variances is calculated as follows:
where \(\bar x_1\) and \(\bar x_2\) are the sample means, \(n_1\) and \(n_2\) are the sample sizes, and \(s_p^2\) is pooled sample variance \(s_p^2\) calculated as:
where \(s_1^2\) and \(s_2^2\) are the sample variances of the two groups. Even if we assume equal variances, we still need to combine the information from both samples to get a more precise estimate of the common variance.
In the Student’s t-test, the standard error of the difference between the means is calculated using the pooled variance as:
This standard error, which incorporates the pooled estimate of the common variance, is used in the denominator of the t-statistic for the Student’s t-test:
The degrees of freedom for the Student’s t-test (assuming equal variances) are \(\mathrm{DF} = n_1 + n_2 - 2\), which directly corresponds to the denominator in the pooled variance formula. This reflects the fact that the pooled variance estimate combines information from both samples, each contributing its degrees of freedom to the final estimate.
# Degrees of freedom for equal variances t-test
df_student = n_old + n_yng - 2
# Calculate pooled variance using the sample variances determined in the previous section
pooled_var = ((n_old-1)*var_old + (n_yng-1)*var_yng) / df_student
# Calculate the pooled standard error
se_pooled = np.sqrt(pooled_var * (1/n_old + 1/n_yng))
# Calculate the Student's t-statistic
t_statistic_student = mean_diff / se_pooled
# Print the results
print(f"t-statistic (Student) = {t_statistic_student:.4f} with \
{df_student} degrees of freedom")
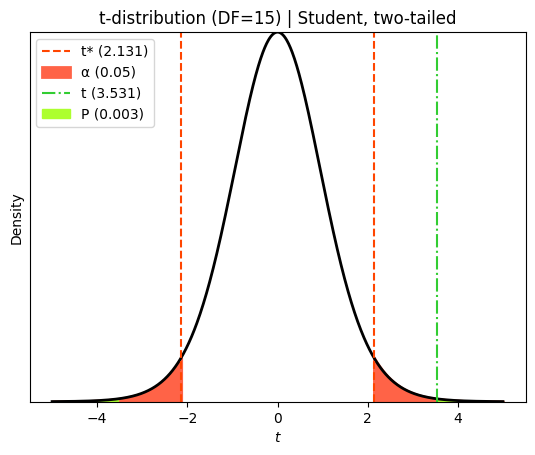
t-statistic (Student) = 3.5315 with 15 degrees of freedom
Special case of equal variances and sample sizes#
In the situation where \(n_1 = n_2 = n\), and \(s_1^2 = s_2^2 = s^2\), with \(n\) the common sample size and \(s^2\) the common sample variance:
Therefore
and \(\mathrm{DF} = 2n -2\).
Student’s P value#
Having calculated the t-statistic and degrees of freedom, we can now determine the P value. Similar to Welch’s t-test, we’ll use the t-distribution’s CDF to compute the P value, which quantifies the probability of observing such an extreme t-statistic (or more extreme) if the null hypothesis were true.
# Calculate the P value using the t-distribution (two-sided test)
p_value_student = 2 * (1 - stats.t.cdf(abs(t_statistic_student), df_student))
# Print the results
print(f"P value for the Student's t-test = {p_value_student:.5f}")
P value for the Student's t-test = 0.00302
Visualizing Student’s values#
To better understand the results of the Student’s t-test, let’s visualize the t-statistic, critical t-values, and the P value areas under the t-distribution. This visual representation will aid in understanding the statistical significance of the observed mean difference and the impact of degrees of freedom on the t-distribution’s shape.
# Calculate critical t-values (two-tailed test)
t_crit_lower_student = stats.t.ppf(alpha/2, df_student)
t_crit_upper_student = stats.t.ppf(1 - alpha/2, df_student)
# Generate x values for plotting
x = np.linspace(-5, 5, 1000)
hx = stats.t.pdf(x, df_student)
# Create the plot
plt.plot(x, hx, lw=2, color="black")
# Plot the critical t-values
plt.axvline(
x=t_crit_lower_student, # type: ignore
color='orangered',
linestyle='--',)
plt.axvline(
x=t_crit_upper_student, # type: ignore
color='orangered',
linestyle='--',
label=f't* ({t_crit_upper_student:.3f})')
# Shade the rejection regions (alpha)
plt.fill_between(
x[x <= t_crit_lower_student],
hx[x <= t_crit_lower_student],
linestyle="-",
linewidth=2,
color='tomato',
label=f'α ({alpha})')
plt.fill_between(
x[x >= t_crit_upper_student],
hx[x >= t_crit_upper_student],
linestyle="-",
linewidth=2,
color='tomato')
# Plot the observed t-statistic
plt.axvline(
x=t_statistic_student,
color='limegreen',
linestyle='-.',
label=f't ({t_statistic_student:.3f})')
# Shade the P-value areas (two-tailed)
plt.fill_between(
x[x <= -abs(t_statistic_student)],
hx[x <= -abs(t_statistic_student)],
color='greenyellow',
label=f'P ({p_value_student:.3f})',)
plt.fill_between(
x[x >= abs(t_statistic_student)],
hx[x >= abs(t_statistic_student)],
color='greenyellow')
# Add labels and title
plt.xlabel(r'$t$')
plt.ylabel('Density')
plt.margins(x=0.05, y=0)
plt.yticks([])
plt.title(f"t-distribution (DF={df_student}) | Student, two-tailed")
plt.legend();
Student’s confidence interval#
The confidence interval for the Student’s t-test follows a similar process as the Welch test, with a key difference in calculating the standard error and degrees of freedom.
Instead of using separate variances for each group, the Student’s t-test assumes equal variances and pools the variance from both groups to estimate a common variance. This pooled variance is then used to calculate the standard error of the difference in means.
Not to forget that the degrees of freedom for the Student’s t-test are simpler to calculate, as they are based on the total sample size of both groups minus 2.
With these adjustments to the standard error and degrees of freedom, the remaining steps to construct the confidence interval are the same as those described for the Welch test.
# Calculate the confidence interval (e.g., 95% confidence)
margin_of_error_student = abs(stats.t.ppf((1 + confidence_level) / 2, df_student)) * se_pooled
ci_student = (mean_diff - margin_of_error_student, mean_diff + margin_of_error_student)
# Print the results
print(f"Mean difference (young - old) = {mean_diff:.3f}")
print(f"95% confidence interval for the mean difference: \
[{ci_student[0]:.3f}, {ci_student[1]:.3f}]")
Mean difference (young - old) = 23.546
95% confidence interval for the mean difference: [9.335, 37.757]
Performing the Student’s t-test in Python#
We can readily perform the Student’s t-test using either scipy.stats or Pingouin. The implementation is nearly identical to Welch’s t-test, with the key difference being that we change the equal_var (in SciPy) or correction (in Pingouin) parameter to explicitly indicate the assumption of equal variances.
# Student's t-test using SciPy (assuming equal variances)
t_statistic_scipy_student, p_value_scipy_student = stats.ttest_ind(yng, old, equal_var=True)
# Student's t-test using Pingouin (assuming equal variances)
ttest_results_pingouin_student = pg.ttest(yng, old, correction=False) # type: ignore
# Print the results
print("Student's t-test results (SciPy):")
print(f"t-statistic = {t_statistic_scipy_student:.3f}, \
P value = {p_value_scipy_student:.4f}")
print("\nStudent's t-test results (Pingouin):")
ttest_results_pingouin_student
Student's t-test results (SciPy):
t-statistic = 3.531, P value = 0.0030
Student's t-test results (Pingouin):
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 3.531488 | 15 | two-sided | 0.003022 | [9.33, 37.76] | 1.715995 | 12.56 | 0.909532 |
Similar to the Welch’s t-test, the Student’s t-test also revealed a statistically significant difference between the two groups. The calculated t-statistic was 3.531, with an associated P value of 0.003. This P value falls below the conventional significance level of 0.05, providing strong evidence to reject the null hypothesis of no difference in the mean \(\%\text{E}_\text{max}\) between the ‘old’ and ‘young’ groups.
The 95% confidence interval for the mean difference (young - old) is [9.335, 37.757]. This interval suggests we can be 95% confident that the true population mean difference in \(\%\text{E}_\text{max}\) lies within this range. The absence of zero within this interval further reinforces the conclusion of a significant difference between the two groups.
Effect size#
Cohen’s d is a widely used effect size measure for unpaired t-tests. It essentially standardizes the difference between the two group means by dividing it by a measure of variability:
However, since we’re dealing with two independent groups, the calculation of the standard deviation (\(s\)) used in the denominator differs slightly depending on whether we assume equal variances or not, as we saw in the Welch and Student t-tests.
# Calculate the standard deviations from the standard errors
sd_unequal = se_unequal * np.sqrt((n_yng * n_old) / (n_yng + n_old)) # For Welch's t-test
sd_pooled = se_pooled * np.sqrt(n_yng + n_old - 2) # For Student's t-test
# Calculate Cohen's d manually
cohens_d_manual_welch = mean_diff / sd_unequal
cohens_d_manual_student = mean_diff / sd_pooled
print(f"Cohen's d (manual, Welch's): {cohens_d_manual_welch:.3f}")
print(f"Cohen's d (manual, Student's): {cohens_d_manual_student:.3f}")
Cohen's d (manual, Welch's): 1.761
Cohen's d (manual, Student's): 0.912
To calculate effect size in various scenarios, including unpaired tests, we can utilize the compute_effsize function provided by the Pingouin library.
# Calculate unbiased Cohen's d using pingouin
effect_size_pingouin = pg.compute_effsize(yng, old, eftype='cohen')
print(f"Unbiased Cohen's d (pingouin): {effect_size_pingouin:.3f}")
Unbiased Cohen's d (pingouin): 1.716
The interpretation guidelines for Cohen’s d in unpaired t-tests are generally the same as those for paired t-tests (discussed in the next chapter):
Small effect: d ≈ 0.2
Medium effect: d ≈ 0.5
Large effect: d ≈ 0.8
Effect size in unpaired t-tests helps understand the practical significance of the findings. A statistically significant result (small P value) doesn’t necessarily mean the effect is large or meaningful. Conversely, a non-significant result might still indicate a meaningful effect, especially if the study has low power due to a small sample size. By considering both the P value and the effect size, we can gain a more complete picture of your results and draw more informed conclusions.
Working with real world data#
Loading the data#
Let’s introduce the Palmer penguins dataset from the Pingouin library and demonstrate how to perform an unpaired t-test directly on its columns. We’ll also explore one-sided t-tests and investigate the relationship between overlapping error bars and the statistical significance of mean differences.

import pandas as pd
# List all available datasets in pingouin (commented out)
# pg.list_dataset()
# Load the 'penguins' dataset
penguins = pg.read_dataset('penguins')
# Display the first 5 rows of the dataset
penguins.head()
| species | island | bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | sex | |
|---|---|---|---|---|---|---|---|
| 0 | Adelie | Biscoe | 37.8 | 18.3 | 174.0 | 3400.0 | female |
| 1 | Adelie | Biscoe | 37.7 | 18.7 | 180.0 | 3600.0 | male |
| 2 | Adelie | Biscoe | 35.9 | 19.2 | 189.0 | 3800.0 | female |
| 3 | Adelie | Biscoe | 38.2 | 18.1 | 185.0 | 3950.0 | male |
| 4 | Adelie | Biscoe | 38.8 | 17.2 | 180.0 | 3800.0 | male |
Understanding the data#
Let’s print some descriptive statistics for the different variables.
# Display descriptive statistics
penguins.describe(include='all')
| species | island | bill_length_mm | bill_depth_mm | flipper_length_mm | body_mass_g | sex | |
|---|---|---|---|---|---|---|---|
| count | 344 | 344 | 342.000000 | 342.000000 | 342.000000 | 342.000000 | 333 |
| unique | 3 | 3 | NaN | NaN | NaN | NaN | 2 |
| top | Adelie | Biscoe | NaN | NaN | NaN | NaN | male |
| freq | 152 | 168 | NaN | NaN | NaN | NaN | 168 |
| mean | NaN | NaN | 43.921930 | 17.151170 | 200.915205 | 4201.754386 | NaN |
| std | NaN | NaN | 5.459584 | 1.974793 | 14.061714 | 801.954536 | NaN |
| min | NaN | NaN | 32.100000 | 13.100000 | 172.000000 | 2700.000000 | NaN |
| 25% | NaN | NaN | 39.225000 | 15.600000 | 190.000000 | 3550.000000 | NaN |
| 50% | NaN | NaN | 44.450000 | 17.300000 | 197.000000 | 4050.000000 | NaN |
| 75% | NaN | NaN | 48.500000 | 18.700000 | 213.000000 | 4750.000000 | NaN |
| max | NaN | NaN | 59.600000 | 21.500000 | 231.000000 | 6300.000000 | NaN |
The culmen is the upper ridge of a bird’s bill. In the simplified penguins data, culmen length and depth are renamed as variables ‘bill_length_mm’ and ‘bill_depth_mm’ to be more intuitive.
For this penguin data, the culmen (bill) length and depth are measured as shown below:

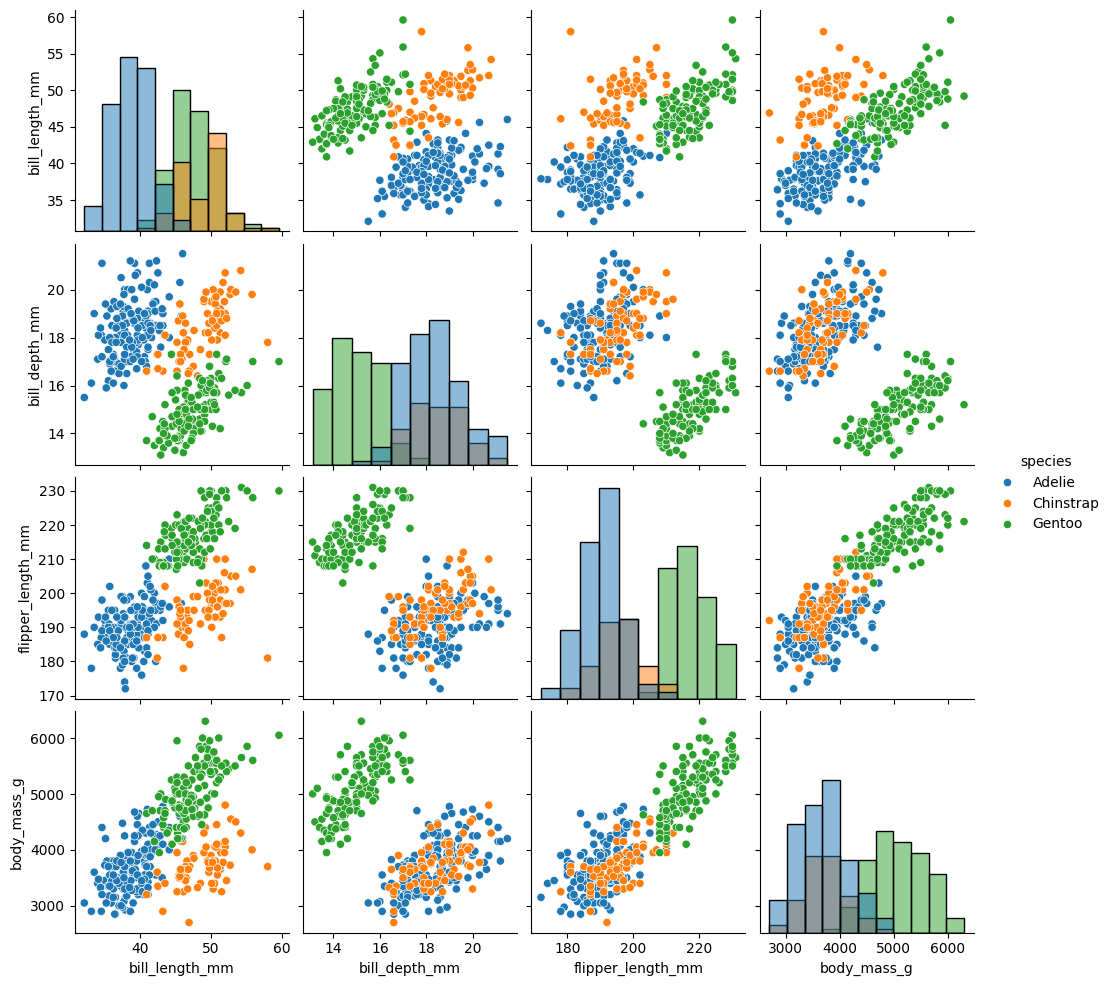
Let’s now create a grid of scatterplots that visualize the relationships between pairs of numerical variables in the penguins DataFrame. It also incorporates color-coded distinctions based on the ‘species’ column and customizes the diagonal plots to display histograms, providing insights into the individual distributions of each variable for each species.
sns.pairplot(penguins, hue="species", diag_kind="hist");
Checking assumptions#
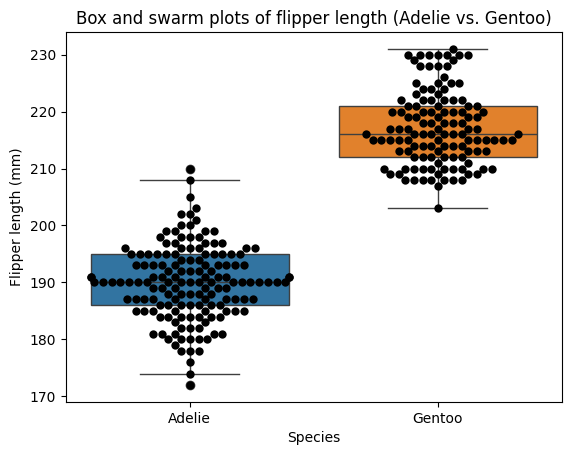
Flipper length appears to be a promising variable for distinguishing between penguin species. Let’s apply the t-test framework we’ve established to investigate this further. To illustrate the concepts clearly, we’ll focus on the two most populous species in the dataset: Adelie and Gentoo. However, it’s important to note that in a comprehensive analysis, we would ideally include all groups and employ ANOVA (which we’ll discuss in a later chapter) to account for potential differences among all species simultaneously.
# Statistics for groups of species
penguins.groupby(by='species')['flipper_length_mm'].describe()
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| species | ||||||||
| Adelie | 151.0 | 189.953642 | 6.539457 | 172.0 | 186.0 | 190.0 | 195.0 | 210.0 |
| Chinstrap | 68.0 | 195.823529 | 7.131894 | 178.0 | 191.0 | 196.0 | 201.0 | 212.0 |
| Gentoo | 123.0 | 217.186992 | 6.484976 | 203.0 | 212.0 | 216.0 | 221.0 | 231.0 |
# Remove the Chinstrap species
# Create a copy to avoid modifying the original DataFrame
penguins_filtered = penguins[penguins['species'] != 'Chinstrap'].copy()
# Box and swarm plots
sns.boxplot(
data=penguins_filtered,
x='species',
y='flipper_length_mm',
hue='species')
sns.swarmplot(
data=penguins_filtered,
x='species',
y='flipper_length_mm',
color='black',
size=6)
plt.xlabel('Species')
plt.ylabel('Flipper length (mm)')
plt.title("Box and swarm plots of flipper length (Adelie vs. Gentoo)");
# Perform tests using our own function (see normality testing)
normality_tests(
adelie_flipper:=penguins_filtered.loc[
penguins_filtered['species'] == 'Adelie', 'flipper_length_mm'].values,
"Adelie penguins")
print('\n')
normality_tests(
gentoo_flipper:=penguins_filtered.loc[
penguins_filtered['species'] == 'Gentoo', 'flipper_length_mm'].values,
"Gentoo penguins")
----Normality tests for Adelie penguins----
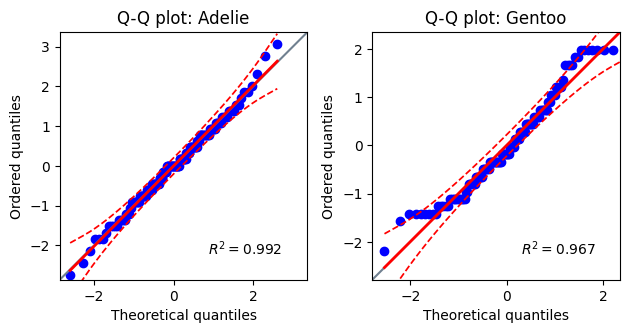
Test W P value normal
D'Agostino-Pearson 1.08 0.582 True
Shapiro-Wilk 0.99 0.720 True
-------------------------------------------
----Normality tests for Gentoo penguins----
Test W P value normal
D'Agostino-Pearson 6.12 0.047 False
Shapiro-Wilk 0.96 0.002 False
-------------------------------------------
# Plotting Q-Q plots
fig, axes = plt.subplots(1, 2)
titles = ["Q-Q plot: Adelie", "Q-Q plot: Gentoo"]
for i, (data, title) in enumerate(zip([adelie_flipper, gentoo_flipper], titles)):
pg.qqplot(
data,
dist='norm',
ax=axes[i],
confidence=0.95,)
axes[i].set_title(title)
plt.tight_layout() # Ensures plots don't overlap
# Levene's test for equal variances
# Note the difference with the method call on a DataFrame compared to arrays
pg.homoscedasticity(
data=penguins_filtered,
dv='flipper_length_mm',
group='species',
method='levene')
| W | pval | equal_var | |
|---|---|---|---|
| levene | NaN | NaN | False |
The problem of missing values#
The Levene’s test returned NaN values and equal_var=False. This discrepancy is unexpected, given the similar standard deviations and sample sizes observed in the descriptive statistics. It’s likely that missing values are causing Levene’s test to fail, as many statistical tests struggle to handle NaN values. Let’s investigate whether the adelie_flipper or gentoo_flipper arrays contain any missing data.
penguins_filtered.info()
<class 'pandas.core.frame.DataFrame'>
Index: 276 entries, 0 to 343
Data columns (total 7 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 species 276 non-null object
1 island 276 non-null object
2 bill_length_mm 274 non-null float64
3 bill_depth_mm 274 non-null float64
4 flipper_length_mm 274 non-null float64
5 body_mass_g 274 non-null float64
6 sex 265 non-null object
dtypes: float64(4), object(3)
memory usage: 17.2+ KB
As there are some missing non-null values in the dataset, and in the ‘flipper_length_mm’ columns in particular, we’ll need to decide how to handle them, e.g., remove rows with missing values, or impute missing values, before running the test again. Let’s drop the rows containing missing values in the ‘flipper_length_mm’ column.
penguins_filtered_clean = penguins_filtered.dropna(subset='flipper_length_mm')
pg.homoscedasticity(
data=penguins_filtered_clean,
dv='flipper_length_mm',
group='species',
method='levene')
| W | pval | equal_var | |
|---|---|---|---|
| levene | 0.157042 | 0.692205 | True |
Performing t-test#
While the flipper length data for Adelie penguins appears to be normally distributed, the Gentoo flipper lengths show some deviation from normality, particularly at the extremes. However, given the relatively large sample sizes (n=151 for Adelie and n=123 for Gentoo), we can proceed with the Student’s t-test (assuming equal variances), acknowledging the potential limitations due to this minor departure from normality. Though, the most appropriate statistical test would be to compare all the groups using ANOVA (discussed in a future chapter).
# Perform Student t-test
pg.ttest(
x=adelie_flipper, # the method removes missing values by default
y=gentoo_flipper,
correction=False # type: ignore
)
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | -34.414958 | 272 | two-sided | 4.211309e-101 | [-28.79, -25.68] | 4.18005 | 1.128e+97 | 1.0 |
The extremely small P value (4.211e-101) is far below the typical significance level of 0.05. This provides overwhelming evidence to reject the null hypothesis of no difference between the two group means.
The 95% confidence interval [-28.79, -25.68] provides a range of plausible values for the true difference between the population means. The fact that this interval doesn’t include zero further supports the conclusion of a significant difference.
Therefore, we can conclude that there is a statistically significant difference between the means of the two groups being compared.
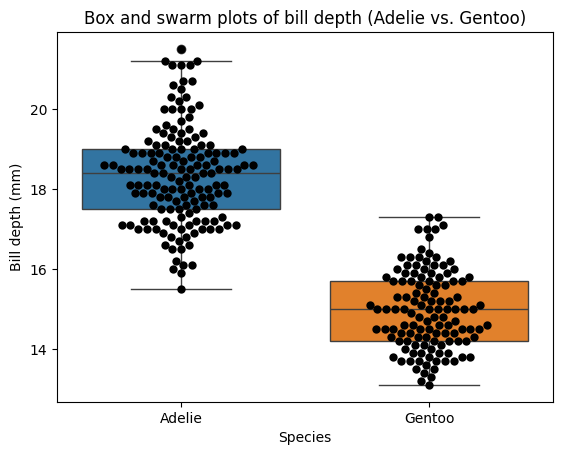
Overlapping distributions#
In the previous example with flipper length, we observed that non-overlapping distributions generally corresponded to a statistically significant difference in means. However, it’s important to remember that overlapping distributions do not necessarily imply the absence of a significant difference. The statistical significance of the mean difference depends on various factors, including the degree of overlap, sample sizes, and the variability within each group.
Let’s examine the ‘bill_depth_mm’ variable for Adelie and Gentoo penguins.
# Box and swarm plots
sns.boxplot(
data=penguins_filtered,
x='species',
y='bill_depth_mm',
hue='species')
sns.swarmplot(
data=penguins_filtered,
x='species',
y='bill_depth_mm',
color='black',
size=6)
plt.xlabel('Species')
plt.ylabel('Bill depth (mm)')
plt.title("Box and swarm plots of bill depth (Adelie vs. Gentoo)");
# Perform Student t-test
pg.ttest(
x=penguins_filtered.loc[penguins_filtered['species'] == 'Adelie', 'bill_depth_mm'],
y=penguins_filtered.loc[penguins_filtered['species'] == 'Gentoo', 'bill_depth_mm'],
correction=False # type: ignore
)
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 24.792495 | 272 | two-sided | 9.311098e-72 | [3.1, 3.63] | 3.011303 | 8.109e+67 | 1.0 |
Furthermore, overlapping error bars do not necessarily imply that the means of the populations are not significantly different. The degree of overlap, the sample sizes, and the variability within each group all play a role in determining statistical significance. It’s always crucial to conduct formal hypothesis tests, like the t-test, to draw valid conclusions about differences between groups.
This observation is particularly relevant when dealing with distributions based on low sample sizes, as their error bars tend to be wider, leading to more overlap even when there might be a true difference in population means. It’s essential to rely on the P value from the t-test rather than solely on visual inspection of error bar overlap, especially when sample sizes are small.
We can use the following rules of thumbs:
Type of error bar |
Overlapping error bars |
Non-overlapping error bars |
|---|---|---|
SD |
No conclusion |
No conclusion |
SEM |
Likely P > 0.05 |
No conclusion |
95% CI |
No conclusion |
Likely P < 0.05 |
One-sided t-test#
In our penguin dataset scenario, we aim to determine if the bill depth of Adelie penguins, after subtracting 3 mm, is still significantly greater than the bill depth of Gentoo penguins. Mathematically, we want to test if: \(\bar x_\text{Adelie} - 3 > \bar x_\text{Gentoo}\). We can restate \(\bar x_{\text{Adelie} - 3} > \bar x_\text{Gentoo}\). This allows us to frame our hypotheses for a one-sided t-test:
Null hypothesis (H0): the mean bill depth of Adelie penguins, minus 3 mm, is equal to or less than the mean bill depth of Gentoo penguins (\(\bar x_\text{Adelie - 3} \le \bar x_\text{Gentoo}\)).
Alternative hypothesis (H1): the mean bill depth of Adelie penguins, minus 3 mm, is greater than the mean bill depth of Gentoo penguins.
Let’s conduct a one-sided t-test on our sample data to evaluate these hypotheses.
# Perform one-sided Student t-test with pingouin
pg.ttest(
x=penguins_filtered.loc[penguins_filtered['species'] == 'Adelie', 'bill_depth_mm'] - 3,
# Missing values are automatically removed from the data in pingouin
y=penguins_filtered.loc[penguins_filtered['species'] == 'Gentoo', 'bill_depth_mm'],
correction=False, # type: ignore
alternative='greater',
)
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 2.684262 | 272 | greater | 0.003858 | [0.14, inf] | 0.326031 | 7.951 | 0.849133 |
# Perform one-sided Student t-test with scipy.stats
stats.ttest_ind(
penguins_filtered.loc[penguins_filtered['species'] == 'Adelie', 'bill_depth_mm'] - 3,
penguins_filtered.loc[penguins_filtered['species'] == 'Gentoo', 'bill_depth_mm'],
equal_var=True,
alternative='greater',
nan_policy='omit', # scipy doesn't remove missing values automatically
)
TtestResult(statistic=2.684262207738359, pvalue=0.003857530781549446, df=272.0)
# Finally statsmodels also offers a comprehensive t-test API
import statsmodels.api as sm
# Perform Student's t-test
ttest_results_sm = sm.stats.ttest_ind(
x1=penguins_filtered_clean.loc[penguins_filtered['species'] == 'Adelie', 'bill_depth_mm'],
# statsmodels doesn't support policy for missing values
x2=penguins_filtered_clean.loc[penguins_filtered['species'] == 'Gentoo', 'bill_depth_mm'],
usevar='pooled', # Specify equal variances assumption
alternative='larger', # Test if the Adelie bill depth mean (x1) is larger
value=3 # difference between the means (x1 - x2) under the null hypothesis
)
# Extract and print the relevant statistics
t_statistic_sm = ttest_results_sm[0]
p_value_sm = ttest_results_sm[1]
df_sm = ttest_results_sm[2]
print(f"Student's t-test results:")
print(f"t-statistic = {t_statistic_sm:.3f}, P value = {p_value_sm:.5f}, DF= {df_sm}")
Student's t-test results:
t-statistic = 2.684, P value = 0.00386, DF= 272.0
Non-parametric methods#
While biological data rarely perfectly adhere to a Gaussian (normal) distribution, many biological variables exhibit an approximately bell-shaped distribution. Parametric tests, such as the t-test and ANOVA, are often robust to minor deviations from normality, especially with large samples. Consequently, these tests are widely used across various scientific disciplines.
Non-parametric methods offer a valuable set of tools for analyzing data when the assumptions of parametric tests, such as the t-test or ANOVA, are not met. Unlike parametric methods that assume the data are sampled from a Gaussian distribution, non-parametric methods do not rely on such strict distributional assumptions. Instead, many of these tests operate by ranking the data from low to high and analyzing these ranks, making them less sensitive (more robust) to outliers and deviations from normality. But when the data is truly Gaussian (normally distributed), non-parametric tests generally have lower statistical power compared to their parametric counterparts. This means they might be less likely to detect a true difference if one exists.
The choice between parametric and non-parametric tests can also be influenced by the sample size:
Distribution |
Test |
Small samples |
Large Samples |
|---|---|---|---|
Gaussian |
Non-parametric |
Misleading, low power |
Nearly as powerful as parametric tests |
Non-Gaussian |
Parametric |
Misleading, not robust |
Robust to mild deviations from normality |
Moreover, reporting confidence intervals for non-parametric tests can be more challenging, and they might not be as readily available or interpretable as those for parametric tests, and extending non-parametric tests to more complex models, such as regression models, can be less straightforward compared to parametric methods.
Below is a flowchart designed to help choosing which functions of Pingouin are adequate for a non-parametric analysis:
Of note, computer-intensive methods like bootstrapping and permutation tests also fall under the non-parametric umbrella, as they don’t assume a specific distribution for the data. These methods provide robust alternatives for estimating P values and confidence intervals, especially when dealing with small sample sizes or non-normal data, and will be discussed in the next section.
Performing the Mann-Whitney U test manually#
Exact method#
The Mann-Whitney U test (also known as the Wilcoxon rank-sum test) is a non-parametric method for comparing two unpaired groups. It assesses whether one group tends to have larger or smaller values than the other. Unlike the t-test, it doesn’t assume that the data follows a normal distribution.
If we have two groups with observations \(x_1, x_2, \dots, x_m\) and \(y_1, y_2, \dots, y_n\) sampled from populations \(X\) and \(Y\), respectively, the Mann-Whitney U/Wilcoxon rank-sum test assesses the null hypothesis that the probability of a randomly selected observation from group \(X\) being greater than a randomly selected observation from group \(Y\) is \(0.5\). Formally:
Under the null hypothesis, \(P(x_i > y_j) = 0.5\), the probability that a randomly selected observation from one group is larger than a randomly selected observation from the other group is equal to 0.5. Essentially, this means the two groups have the same distribution.
Under the alternative hypothesis, \(P(x_i > y_j) \ne 0.5\), the probability that a randomly selected observation from one group is larger than a randomly selected observation from the other group is not equal to 0.5, implying that the two groups have different distributions.
How do the test works concretely:
Combine and rank: combine the data from both groups and rank the values from lowest to highest, ignoring the group labels
Calculate rank sums: calculate the sum of the ranks for each group. We assign the median rank to tied values (mid-rank method)
Calculate \(U\) statistic: the U statistic is calculated for each group based on the rank sums, sample sizes, and a correction factor for ties (if any). Specifically, the formulas for the U statistics are:
\(U_x = mn + \frac{m(m+1)}{2} - R_x\)
\(U_y = mn + \frac{n(n+1)}{2} - R_y\)
where \(m\) is the number of samples drawn from population \(X\), \(n\) is the number of samples drawn from population \(Y\), and \(R_x\) and \(R_y\) are the sum of the ranks attributed to population \(X\) and \(Y\), respectively.
The final \(U\) statistic used for the test is the minimum of the two: \(U = \min(U_x, U_y)\)
Determine significance: \(U\) is compared to a critical value from a Mann-Whitney U table (for the chosen significance level and sample sizes). If the calculated \(U\) value is less than or equal to the critical value (\(U \leq U^\ast\)), we reject the null hypothesis. Otherwise, we fail to reject the null hypothesis.
from scipy.stats import rankdata
# Combine the data
combined_data = np.concatenate((old, yng))
# Rank the data
ranks = rankdata(combined_data)
# 'average' method used to assign ranks to tied elements by default
# Separate the ranks for each group
old_ranks = ranks[:len(old)]
yng_ranks = ranks[len(old):]
# Calculate the rank sums
R1 = np.sum(old_ranks)
R2 = np.sum(yng_ranks)
# Calculate the U statistic for each group
n1 = len(old)
n2 = len(yng)
U1 = n1 * n2 + (n1 * (n1 + 1)) / 2 - R1
U2 = n1 * n2 + (n2 * (n2 + 1)) / 2 - R2
# Determine the U statistic
U_statistic = min(U1, U2)
# Critical U value for n1=9 and n2=8 with alpha=0.05 from the table
# https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_nonparametric/Mann-Whitney-Table-CriticalValues.pdf
U_critical = 15
# Print the results
print(f"U1 = {U1:n}")
print(f"U2 = {U2:n}")
print(f"U = {U_statistic:n}")
print(f"U* (n={n1}, m={n2}, alpha=0.05) = {U_critical:n}")
# Compare U to the critical value and draw a conclusion
if U_statistic <= U_critical:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
U1 = 65
U2 = 7
U = 7
U* (n=9, m=8, alpha=0.05) = 15
Reject the null hypothesis. There is a significant difference between the groups.
The Mann-Whitney U test’s critical values table is generated from the probability distribution of the U statistic, as detailed in the original paper by Mann and Whitney. They used a recursion relation to define this distribution:
Python readily supports recursive functions, providing a concise and elegant way to implement algorithms that involve repeated self-reference.
def mann_whitney_u_prob(U, n, m):
"""
Calculate the probability of a specific U value in the Mann-Whitney U distribution.
Args:
U: The U statistic value.
n: The number of observations in the first group.
m: The number of observations in the second group.
Returns:
The probability of the U value.
"""
if n == 0 or m == 0:
return 1 if U == 0 else 0
elif n > 0 and m > 0:
return (n * mann_whitney_u_prob(U - m, n - 1, m) + m * mann_whitney_u_prob(U, n, m - 1)) / (n + m)
else:
return 0 # Handle invalid input (negative n or m)
# Using the current data
probability = mann_whitney_u_prob(U_statistic, n1, n2)
print(f"P(U={U_statistic}, n={n1}, m={n2}) = {probability:.4f}")
P(U=7.0, n=9, m=8) = 0.0006
To gain a deeper understanding of the underlying probability distribution of the U statistic, let’s generate a table that illustrates the exact probabilities for various combinations of sample size \(m\) and \(U\) values, with \(n\) fixed. This table will provide insights into the behavior of the U statistic under different scenarios and help us appreciate the complexities involved in calculating the exact P values for the Mann-Whitney U test.
# Generate the table for n = 9
n = n1
U_values = range(10) # U from 0 to 9
m_values = range(1, 10) # m from 1 to 9
table_data = {}
for m in m_values:
row_data = {}
for U in U_values:
row_data[U] = mann_whitney_u_prob(U, n, m)
table_data[m] = row_data
df = pd.DataFrame(table_data)
df.columns.name="m"
df.index.name="U"
# Display the table
pg.print_table(df, floatfmt='.6f')
1 2 3 4 5 6 7 8 9
-------- -------- -------- -------- -------- -------- -------- -------- --------
0.100000 0.018182 0.004545 0.001399 0.000500 0.000200 0.000087 0.000041 0.000021
0.100000 0.018182 0.004545 0.001399 0.000500 0.000200 0.000087 0.000041 0.000021
0.100000 0.036364 0.009091 0.002797 0.000999 0.000400 0.000175 0.000082 0.000041
0.100000 0.036364 0.013636 0.004196 0.001499 0.000599 0.000262 0.000123 0.000062
0.100000 0.054545 0.018182 0.006993 0.002498 0.000999 0.000437 0.000206 0.000103
0.100000 0.054545 0.022727 0.008392 0.003497 0.001399 0.000612 0.000288 0.000144
0.100000 0.072727 0.031818 0.012587 0.004995 0.002198 0.000962 0.000452 0.000226
0.100000 0.072727 0.036364 0.015385 0.006494 0.002797 0.001311 0.000617 0.000309
0.100000 0.090909 0.045455 0.020979 0.008991 0.003996 0.001836 0.000905 0.000452
0.100000 0.090909 0.054545 0.025175 0.011489 0.005195 0.002448 0.001193 0.000617
The P value represents the probability of observing a U value as extreme as, or more extreme than, the one calculated from the data, assuming the null hypothesis is true. The cumulative distribution function (CDF) provides this information: by summing the probabilities in all the rows above a cell in a given column in the U table, we are effectively calculating the probability of obtaining a U value less than or equal to the value represented by that cell. This cumulative probability is then used to determine the P value for the test. Below is the cumulative distribution table derived from the previous table.
# Calculate the cumulative sum of probabilities along the rows (axis=0)
df.cumsum(axis=0)
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| U | |||||||||
| 0 | 0.1 | 0.018182 | 0.004545 | 0.001399 | 0.000500 | 0.000200 | 0.000087 | 0.000041 | 0.000021 |
| 1 | 0.2 | 0.036364 | 0.009091 | 0.002797 | 0.000999 | 0.000400 | 0.000175 | 0.000082 | 0.000041 |
| 2 | 0.3 | 0.072727 | 0.018182 | 0.005594 | 0.001998 | 0.000799 | 0.000350 | 0.000165 | 0.000082 |
| 3 | 0.4 | 0.109091 | 0.031818 | 0.009790 | 0.003497 | 0.001399 | 0.000612 | 0.000288 | 0.000144 |
| 4 | 0.5 | 0.163636 | 0.050000 | 0.016783 | 0.005994 | 0.002398 | 0.001049 | 0.000494 | 0.000247 |
| 5 | 0.6 | 0.218182 | 0.072727 | 0.025175 | 0.009491 | 0.003796 | 0.001661 | 0.000782 | 0.000391 |
| 6 | 0.7 | 0.290909 | 0.104545 | 0.037762 | 0.014486 | 0.005994 | 0.002622 | 0.001234 | 0.000617 |
| 7 | 0.8 | 0.363636 | 0.140909 | 0.053147 | 0.020979 | 0.008791 | 0.003934 | 0.001851 | 0.000926 |
| 8 | 0.9 | 0.454545 | 0.186364 | 0.074126 | 0.029970 | 0.012787 | 0.005769 | 0.002756 | 0.001378 |
| 9 | 1.0 | 0.545455 | 0.240909 | 0.099301 | 0.041459 | 0.017982 | 0.008217 | 0.003949 | 0.001995 |
For instance, if the calculated U statistic is 7, and the corresponding probability for n = 9 and m = 8 is 0.00185, which is less than 0.05/2 = 0.025 (for a two-sided test), we reject the null hypothesis. This indicates a significant difference in the medians of the two groups.
# Display the cumulative probability for U=7 and m=8 (n=9)
cumulative_prob = df.cumsum(axis=0).loc[7, 8].item() # type: ignore
p_value = 2 * cumulative_prob # Multiply by 2 for two-tailed test
print(f"Cumulative probability for U=7 and m=8 (n=9): {cumulative_prob:.5f}")
print(f"P value (two-tailed): {p_value:.7f}")
# Compare the p-value to 0.05
if p_value < 0.05:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
Cumulative probability for U=7 and m=8 (n=9): 0.00185
P value (two-tailed): 0.0037022
Reject the null hypothesis. There is a significant difference between the groups.
One practical advantage of non-parametric tests is their ability to handle data that contains values that are too high or too low to be precisely measured. In such cases, where exact quantification is impossible, we can assign arbitrary very low or very high values to these data points. Since non-parametric tests focus on the relative ranks of the data rather than their precise magnitudes, the test results won’t be affected by the lack of exact values for these extreme measurements.
Asymptotic approach#
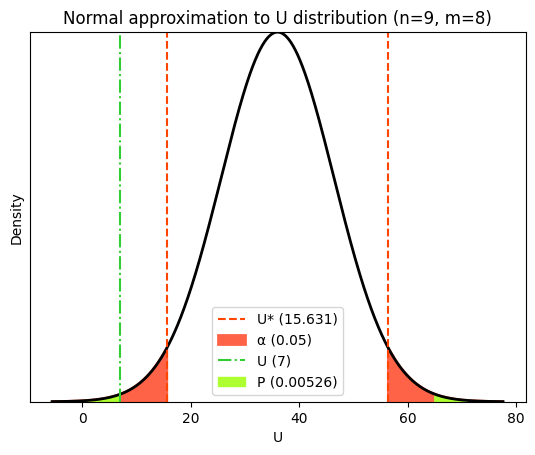
While statistical packages offer accurate calculations for the Mann-Whitney U test, visualizing its exact distribution can be complex. As an alternative, we can explore the asymptotic distribution (normal approximation) for visualization purposes. Keep in mind that this approximation might not be ideal for small samples, but it effectively illustrates the distribution’s shape and how the P value is computed.
In fact, for larger sample sizes, the distribution of the U statistic under the null hypothesis can be approximated by a normal distribution. This approximation simplifies the calculation of P values and makes it easier to visualize the distribution.
To define this approximate normal distribution, we need to know its mean and standard deviation. These parameters are calculated based on the sample sizes of the two groups being compared. The mean of the normal approximation is used to center the distribution curve on the plot. This helps in visually comparing the observed U statistic to the expected distribution under the null hypothesis. The mean and standard deviation are also used in the calculation of the z-score, which is then used to determine the P value based on the standard normal distribution.
from scipy.stats import norm
# Determine the meean and SD to approximate the distribution
μ = n1 * n2 / 2
σ = np.sqrt(n1 * n2 * (n1 + n2 + 1) / 12) # Based on the variance of rank sum
# Generate x values for plotting the normal distribution
x = np.linspace(μ - 4 * σ, μ + 4 * σ, 1000)
normal_pdf = norm.pdf(x, loc=μ, scale=σ)
# Create the plot
plt.plot(x, normal_pdf, lw=2, color="black")
# Plot the critical U-values (two-tailed test)
U_crit_lower = μ - norm.ppf(1 - alpha/2) * σ
U_crit_upper = μ + norm.ppf(1 - alpha/2) * σ
# Calculate the z-score
z_score = (U_statistic - μ) / σ
# Calculate the p-value (two-tailed)
p_value_U = 2 * (1 - norm.cdf(abs(z_score)))
plt.axvline(
x=U_crit_lower,
color='orangered',
linestyle='--')
plt.axvline(
x=U_crit_upper,
color='orangered',
linestyle='--',
label=f"U* ({U_crit_lower:.3f})")
# Shade the rejection regions (alpha)
plt.fill_between(
x,
normal_pdf,
where=(x <= U_crit_lower) | (x >= U_crit_upper),
linestyle="-",
linewidth=2,
color='tomato',
label=f'α ({alpha})')
# Plot the observed U-statistic
plt.axvline(
x=float(U_statistic),
color='limegreen',
linestyle='-.',
label=f'U ({U_statistic:n})')
# Shade the P-value areas (two-tailed)
plt.fill_between(
x,
normal_pdf,
where=(x <= U_statistic) | (x >= μ + (μ - U_statistic)),
color='greenyellow',
label=f"P ({p_value_U:.5f})")
# Add labels and title
plt.xlabel('U')
plt.ylabel('Density')
plt.margins(x=0.05, y=0)
plt.yticks([])
plt.title(f"Normal approximation to U distribution (n={n1}, m={n2})")
plt.legend();
Python tools for non-parametric unpaired t-test#
Python offers convenient and powerful tools for performing the Mann-Whitney U test, simplifying the analysis and providing additional functionalities.
SciPy provides a comprehensive collection of statistical functions, including the mannwhitneyu function for performing the Mann-Whitney U test.
from scipy.stats import mannwhitneyu
# Perform Mann-Whitney U test with exact p-value calculation
U_statistic_exact, p_value_exact = mannwhitneyu(old, yng, method='exact')
# Perform Mann-Whitney U test with asymptotic (normal approximation) p-value calculation
U_statistic_asymptotic, p_value_asymptotic = mannwhitneyu(old, yng, method='asymptotic', use_continuity=False)
# method='auto' choose between the 'asymptotic' and 'exact' based on the sample sizes and the presence of ties
# Print the results
print("Mann-Whitney U test results:")
print(f"Exact P value: {p_value_exact:.5f}")
print(f"Asymptotic P value: {p_value_asymptotic:.5f}")
Mann-Whitney U test results:
Exact P value: 0.00370
Asymptotic P value: 0.00523
Pingouin’s mwu function provides a more comprehensive output, including additional statistics like the rank biserial correlation and the common language effect size. These statistics offer further insights into the magnitude and direction of the difference between the two groups, complementing the P value obtained from the test, but won’t be disscussed here.
pg.mwu(old, yng, method='asymptotic', use_continuity=False, alternative='two-sided')
| U-val | alternative | p-val | RBC | CLES | |
|---|---|---|---|---|---|
| MWU | 7.0 | two-sided | 0.005234 | -0.805556 | 0.097222 |
When the P value is less than 0.05 in a two-tailed Mann-Whitney U test, using both exact and asymptotic methods, we can conclude that there is a significant difference between the two groups being compared. This means that the probability of observing the data (or more extreme data) if the null hypothesis were true is less than 5%. Therefore, we reject the null hypothesis, and conclude that there is a difference in the distribution between the two groups.
Bootstrapping and permutation tests#
Bootstrapping offers a powerful alternative for statistical inference, allowing us to estimate parameters and confidence intervals directly from the data itself, without relying on strong assumptions about the underlying population distribution. This approach, also known as non-parametric inference, was previously encountered in the chapter on calculating the confidence interval of a mean (univariate).
While bootstrapping is primarily used for estimation, permutation tests, another resampling-based method, are specifically designed for hypothesis testing. They can be employed to test various hypotheses, such as the null hypothesis of exchangeability (where group labels are irrelevant) or the hypothesis of equal means after shifting the group means to a common value.
The essence of bootstrapping#
The core idea behind bootstrapping is to treat our observed sample as miniature representation of the population. We repeatedly resample from our original sample to create multiple bootstrap samples. Each replicate is generated by randomly sampling (with replacement) from the original data, creating a new dataset of the same size.
The power of bootstrapping lies in its ability to empirically estimate the sampling distribution of a statistic of interest, such as the difference between group means. By calculating this statistic for each bootstrap sample, we generate a bootstrap distribution. This distribution serves as an approximation of how the statistic would vary if we were to repeatedly sample from the population. It’s important to note that while the central limit theorem guarantees that the distribution of sample means approaches a normal distribution as the sample size increases, with \(\bar X \sim \mathcal N(\mu, \frac{\sigma^2}{\sqrt{n}})\), bootstrapping doesn’t rely on this assumption. It directly leverages the empirical distribution of the data to make inferences. Learn more on bootstrap and computer-intensive methods in Wilcox (2010) and Manly and Navarro Alberto (2020).
For now, let’s return to the example of bladder muscle relaxation in old and young rats, where we have relatively small sample sizes. This scenario provides an excellent opportunity to showcase the power and utility of bootstrapping and permutation tests in handling such data limitations.
# Set random seed for reproducibility
np.random.seed(111)
# Generate 10,000 bootstrap replicates of the mean for each group
# !Make sure to choose exactly N elements randomly **with replacement**
n_replicates = 10000
bs_old_means = np.array([
np.mean(
np.random.choice(
old,
size=len(old),
replace=True
)) for _ in range(n_replicates)
])
bs_yng_means = np.array([
np.mean(np.random.choice(yng, size=len(yng), replace=True)) for _ in range(n_replicates)
])
# Calculate the difference between the bootstrap means for each replicate
# (cast operation on numpy arrays)
bs_mean_diff = bs_yng_means - bs_old_means
print(bs_mean_diff[:10]) # print the 10 first replicates
[25.07916667 23.89166667 22.01944444 29.45277778 23.34027778 26.37083333
22.95277778 19.46666667 27.01388889 27.89444444]
Estimate of the confidence interval#
Once we have the bootstrap distribution, we can estimate the confidence interval by finding the percentiles corresponding to the desired confidence level.
For a 95% confidence interval, we typically use the 2.5th and 97.5th percentiles of the bootstrap distribution. This means that 95% of the bootstrap estimates fall within this interval, providing a range of plausible values for the true population parameter. And as seen in the chapter about the confidence interval of a mean, i.e., the confidence interval of the distribution of an unique sample, we can determine the bootstrap standard error as the standard deviation of the bootstrapped distribution of the mean difference.
# Calculate the 95% CI using np.percentile and the standard error
bs_m = np.mean(bs_mean_diff)
bs_CI = np.round(np.percentile(bs_mean_diff, [2.5, 97.5]), 2)
bs_s = np.std(bs_mean_diff, ddof=1)
# Print the results
print(f"Bootstrap estimate of the mean difference = {bs_m:5.2f}")
print(f"95% bootstrap percentile CI = {bs_CI}")
print(f"Bootstrap standard error = {bs_s:.5f}")
Bootstrap estimate of the mean difference = 23.44
95% bootstrap percentile CI = [11.52 35.54]
Bootstrap standard error = 6.07867
It’s generally expected that the confidence interval obtained through bootstrapping, here [11.52, 35.54], will be reasonably similar to the confidence interval calculated using the t-distribution, i.e., [9.335, 37.76], especially when the sample size is sufficiently large, and the underlying assumptions of the t-test are met. Interestingly, the confidence interval obtained through bootstrapping is narrower than the one derived from the t-distribution, despite having lower sample sizes. This might seem counterintuitive, as we generally expect wider confidence intervals with smaller sample sizes due to increased uncertainty.
# Plot the histogram of the bootstrap distribution
plt.hist(
bs_mean_diff,
density=False,
bins='auto', # or use bins=int(n_replicates**.5)
color='gold',
# alpha=.75,
label=r'Resampled $\bar x - \bar y$')
# Annotate the observed mean difference
plt.axvline(
x=mean_diff.item(),
color='cornflowerblue',
linestyle='-', lw=2,
label=fr'Observed $\bar x - \bar y$ ({mean_diff:.3f})')
# Add lines for the confidence interval
plt.axvline(
x=bs_CI[0],
color='red',
linestyle='--',
label=f'2.5th ({bs_CI[0]:.2f})')
plt.axvline(
x=bs_CI[1],
color='red',
linestyle='--',
label=f'97.5th ({bs_CI[1]:.2f})')
# Add labels and title
plt.xlabel('Mean difference')
plt.ylabel('Frequency')
plt.title(f"Bootstrap distribution of mean differences (B={n_replicates})")
plt.legend();
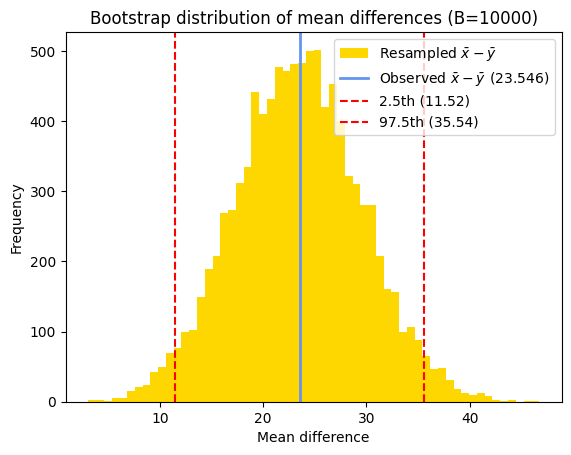
Given the symmetrical distribution of our bootstrapped mean differences, we can also efficiently estimate the confidence interval for the mean difference using the normal approximation and the previously calculated bootstrap standard error.
# Calculate the 95% normal margin of error
z_crit = norm.ppf(0.975)
bs_w = z_crit * bs_s
# Calculate confidence interval
bs_ci_normal = np.round((bs_m - bs_w, bs_m + bs_w), 5)
# Print the result
print(f"95% normal percentile CI of bootstrap distribution = {bs_ci_normal}")
95% normal percentile CI of bootstrap distribution = [11.52206 35.35001]
Bootstrapping relies entirely on the data in the original sample. If, by chance, the original samples have less variability or happen to be more representative of their respective populations, the bootstrap distribution might exhibit less spread, leading to a narrower confidence interval. And as bootstrapping involves random resampling, which introduces some inherent variability in the results, it’s possible that the particular set of bootstrap samples generated in this instance led to a slightly narrower confidence interval than the theoretical one based on the t-distribution. Moreover, the t-distribution-based confidence interval assumes that the data follows a normal distribution. If the actual data deviates from normality, especially in the tails, the t-distribution might overestimate the variability, resulting in a wider confidence interval than necessary.
Bootstrapping with pingouin#
The compute_bootci method from the Pingouin library proves to be a valuable asset in such scenarios, as it streamlines the process of generating confidence intervals using bootstrapping. It eliminates the need for manual creation of bootstrap samples, offering a variety of methods for confidence interval computation, including the normal approximation, percentile bootstrap, and bias-corrected percentile method. Additionally, it provides the flexibility to return the entire bootstrap distribution, enabling further exploration and visualization of the resampling results.
# Calculate 95% percentile bootstrap confidence interval using pingouin
bs_ci, bt = pg.compute_bootci(
x=yng,
y=old,
func=lambda x,y : np.mean(x) - np.mean(y),
confidence=0.95,
method='per',
seed=111,
decimals=3,
n_boot=10000,
return_dist=True)
print(
f"95% percentile bootstrap confidence interval (pingouin): ({bs_ci[0]:.3f}, {bs_ci[1]:.3f})")
bt[:10]
95% percentile bootstrap confidence interval (pingouin): (11.349, 35.713)
array([21.42361111, 21.01527778, 35.11944444, 34.98194444, 16.35555556,
18.95555556, 29.72083333, 19.16944444, 22.78333333, 25.49027778])
Bootstrap P value#
Bootstrapping and permutation tests offer remarkable flexibility in hypothesis testing, going beyond the traditional t-statistic used in t-tests. As we’ve seen, resampling techniques can generate data for constructing confidence intervals around various test statistics. But we can also strategically manipulate the data to simulate the null hypothesis, enabling us to compute P values that assess the likelihood of observing our data under the assumption of no effect.
The key is to choose a test statistic that is relevant to the hypothesis being tested and calculate it consistently for both the original data and the resampled or permuted data. For instance, when the primary goal is to compare the means of two groups, the mean difference or a t-statistic can serve as simple and effective test statistics. However, the flexibility of resampling methods allows us to explore other relevant statistics as well. We can examine the median difference when dealing with skewed data or outliers, the ratio of means for assessing relative differences, or even differences in specific quantiles to capture distributional characteristics. Furthermore, if the research question extends beyond comparing means and focuses on the overall difference in distributions, statistics like the Kolmogorov-Smirnov statistic can be employed within the bootstrapping or permutation framework.
The choice of test statistic in bootstrapping or permutation tests depends on the specific hypothesis being tested and the characteristics of the data. For example, to test the null hypothesis that two groups have the same distribution \(H_0: F(t) = G(t)\), where \(F\) and \(G\) are the cumulative distribution functions, we might shift the data in each group to a common mean, assuming they have equal variances. Alternatively, if we want to test the more general null hypothesis of equal means \(H_0: \mu_X = \mu_Y\) while allowing for unequal variances, we could center each group’s data around zero.
The adaptability of bootstrapping and permutation tests empowers researchers to tailor their analyses precisely to the requirements of their study, providing a robust and versatile approach to statistical inference.
Bootstrapped t-statistics of shifted data#
Bradley Efron proposes an elegant bootstrapping algorithm for comparing the means of two independent samples, even when their overall distribution and variances might differ. This approach involves shifting or centering the data in each group to have a common mean, effectively simulating the null hypothesis of equal population means.
Specifically, we create two new datasets where the values are shifted as follows: \(x_{1i}' = x_{1i} - \bar x_1 + \bar z\), and \(x_{2i}' = x_{2i} - \bar x_2 + \bar z\), where \(\bar z\) is the mean of the combined sample. Next, we perform the following steps \(B\) times (e.g., \(B = 10000\)):
Draw a bootstrap sample \(x_{1i}^b\) of size \(n_1\) with replacement from \(x_{1i}'\)
Draw another bootstrap sample \(x_{2i}^b\) of size \(n_2\) with replacement from \(x_{2i}'\)
Calculate Welch’s t-statistic \(T_i\) using the bootstrap samples. This approach is more robust as it accounts for potential differences in variances between the groups, unlike the Student’s t-statistic, which assumes equal variances.
One-tailed P value#
To estimate the P value using bootstrapping, we assess how often the bootstrapped t-statistics (\(T^b_i\)) are as extreme as, or more extreme than, the observed t-statistic (\(t\)) from our original data. This involves generating multiple bootstrap samples, calculating the t-statistic for each, and determining the proportion of these bootstrap t-statistics that exceed the observed t-statistic.
Mathematically, the bootstrap P value (\(p_B\)) can be expressed as:
But we’re not just interested in any difference, but a difference in a specific direction. A positive statistic suggests an effect in one direction, a negative statistic suggests an effect in the opposite direction. Therefore, if the observed test statistic is negative, i.e., H0: t ≥ 0 and H1: t < 0, the P value is the proportion of bootstrapped test statistics that are less than or equal to the observed test statistic:
where \(I\{\text{condition}\} = 1\) if the condition is true and \(0\) otherwise.
While it’s sometimes suggested to add 1 to both the numerator and denominator of the P value calculation in permutation tests to avoid a P value of 0, there’s no firm consensus on this practice. Some argue it can lead to a slightly more conservative P value, while others consider it an unnecessary adjustment.
Estimating two-tailed bootstrap P value#
Assume \(t > 0\), then we can calculate the probability of observing something as or more extreme in each tail as \(P(T^b \ge t | H_0)\), i.e., what we observed, and \(P(T^b \le -t | H_0)\), i.e., as or more extreme in other tail. For two-sided P values, multiple strategies exist in our bootstrap distribution:
Multiply the highest P value by 2: \(p_B = 2 \times \max[P(T^b \ge t | H_0), P(T^b \le -t | H_0)]\). This is the most conservative strategy.
Multiply the lowest P value by 2: \(p_B = 2 \times \min[P(T^b \ge t | H_0), P(T^b \le -t | H_0)]\). This is the least conservative strategy.
Multiply le lowest one-tailed P value by 2: \(p_B = 2 \times \min[P(T^b \ge t | H_0), P(T^b < t | H_0)]\).
Add the two tails together: \(p_B = P(T^b \ge t | H_0) + P(T^b \le -t | H_0)\). This strategy doesn’t assume symmetry of the bootstrap distribution, so it’s the most flexible one.
99 rule#
When determining the number of bootstrap replicates, we can refer to the “99 rule” suggested by Boos and Stefanski. This rule of thumb proposes that 99 replicates are often sufficient for constructing reliable confidence intervals, especially when estimating the median. However, the optimal number can vary, and for most analyses, especially those involving means or standard deviations, it’s generally recommended to use at least 1,000 replicates. In our subsequent analyses, we’ll use B = 9999 to ensure adequate precision.
# Set the random seed for reproducibility
np.random.seed(111)
n_replicates = 10**4 - 1 # 99 rule
# Calculate the combined mean of both groups
combined_mean = np.mean(np.concatenate([old, yng]))
# Shift the data in each group to have the same mean (combined_mean)
old_shifted = old - np.mean(old) + combined_mean
yng_shifted = yng - np.mean(yng) + combined_mean
# Generate B bootstrap replicates for each shifted group
bs_shifted_old = np.array([
np.random.choice(old_shifted, size=len(old), replace=True) for _ in range(n_replicates)])
bs_shifted_yng = np.array([
np.random.choice(yng_shifted, size=len(yng), replace=True) for _ in range(n_replicates)])
# Calculate sample means and variances for each bootstrap replicate
# !np.mean calculates the mean of the entire flattened array by default if no 'axis' is provided
bs_shifted_old_means = np.mean(bs_shifted_old, axis=1) # Calculate mean along each row/replicate
bs_shifted_yng_means = np.mean(bs_shifted_yng, axis=1)
bs_shifted_old_vars = np.var(bs_shifted_old, ddof=1, axis=1) # Calculate variance along each row
bs_shifted_yng_vars = np.var(bs_shifted_yng, ddof=1, axis=1)
# Calculate the standard error for the difference means for each replicate using Welch's formula
bs_se_unequal = np.sqrt(bs_shifted_old_vars / len(old) + bs_shifted_yng_vars / len(yng))
# Calculate Welch's t-statistic for each bootstrap replicate
bs_t_statistic_welch = (bs_shifted_yng_means - bs_shifted_old_means) / bs_se_unequal
# Or simply perform a Welch's t-test on the bootstrap replicates without calculating intermediates
# bs_t_statistic_welch = np.array([
# stats.ttest_ind(yng, old, equal_var=False)[0] for yng, old in zip(bs_shifted_yng, bs_shifted_old)
# ])
# Print the first 15 t-statistics from the bootstrap replicates
print(bs_t_statistic_welch[:15])
[-0.28169183 0.09257722 -0.72309354 0.9685118 0.9869254 -0.39840539
-0.89747736 -0.84256454 0.74883099 0.72440274 -1.14597461 0.04187397
-1.25776734 0.47912576 0.70211139]
# Calculate one-sided P value using bootstrapping, considering the direction of the observed statistic
# 1. Calculate lower and upper tail
if t_statistic_welch >= 0:
# p_value_bs_shifted_low = np.sum(bs_t_statistic_welch >= t_statistic_welch) / len(bs_t_statistic_welch)
p_value_bs_shifted_up = np.mean(bs_t_statistic_welch >= t_statistic_welch) # Mathematically same as above
p_value_bs_shifted_low = np.mean(bs_t_statistic_welch <= -t_statistic_welch)
else:
p_value_bs_shifted_low = np.mean(bs_t_statistic_welch <= t_statistic_welch)
p_value_bs_shifted_up = np.mean(bs_t_statistic_welch >= -t_statistic_welch)
# 2. Attribute the one-tailed P value
p_value_bs_shifted_1t = p_value_bs_shifted_up if t_statistic_welch >= 0 else p_value_bs_shifted_low
# Print the P value
print(f"One-sided P value obtained using bootstrapped t-statistics = {p_value_bs_shifted_1t:.4f}")
One-sided P value obtained using bootstrapped t-statistics = 0.0023
We can visualize the P value by plotting the histogram of bootstrapped t-statistics (after shifting the data to a common mean). The P value corresponds to the area under the histogram where the t-statistic is greater than or equal to the observed t-statistic.
import matplotlib.patches as mpatches
# Plot the histogram of the bootstrap t-statistics
hist, bins, patches = plt.hist(
bs_t_statistic_welch,
density=False,
bins=int(n_replicates**.5),
color='gold',
# alpha=0.75,
label='Bootstrap t')
# Annotate the observed t-statistic
plt.axvline(
x=t_statistic_welch,
color='limegreen',
linestyle='-.', lw=2,
label=f'Observed t ({t_statistic_welch:.3f})')
# Determine the direction of the observed statistic and plot accordingly
if t_statistic_welch >= 0:
# Plot the histogram of the bootstrap t-statistics >= observed t-statistic
extreme_t_stats = bs_t_statistic_welch[bs_t_statistic_welch >= t_statistic_welch]
# Change the color of the bars based on the direction parameter
for i, bin_edge in enumerate(bins[:-1]):
if np.any(bin_edge >= extreme_t_stats):
patches[i].set_facecolor('lime') # type: ignore
else:
# Plot the histogram of the bootstrap t-statistics <= observed t-statistic
extreme_t_stats = bs_t_statistic_welch[bs_t_statistic_welch <= t_statistic_welch]
for i, bin_edge in enumerate(bins[:-1]):
if np.any(bin_edge <= extreme_t_stats):
patches[i].set_facecolor('lime') # type: ignore
# Add labels and title
plt.xlabel('t')
plt.ylabel('Frequency')
plt.title(f"Bootstrap distribution of Welch's t under H0 (B={n_replicates})")
# Create a copy of the original patch for the legend
original_patch = mpatches.Patch(color='gold', label='Bootstrap t')
# Create a patch for the legend
p_value_patch = mpatches.Patch(color='lime', label=f'One-tailed P ({p_value_bs_shifted_1t:.4f})')
# Add the patches to the legend
plt.legend(handles=[original_patch, plt.gca().lines[0], p_value_patch]); # type: ignore
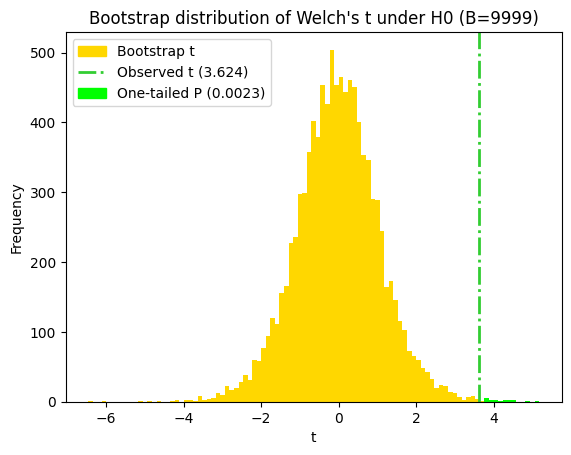
To calculate the two-tailed P value, we typically sum the probabilities in both tails of the distribution. However, since the bootstrap distribution under the null hypothesis is symmetrical, we can also obtain the two-sided P value by simply doubling the more conservative of the two one-tailed P values.
# Maximum one-tail
p_value_bs_shifted_2t_max = 2 * max(p_value_bs_shifted_low, p_value_bs_shifted_up)
# Sum of the tails
p_value_bs_shifted_2t_sum = p_value_bs_shifted_low + p_value_bs_shifted_up
# Print the results
print(f"Two-tailed t-test bootstrap P value (conservative) = {p_value_bs_shifted_2t_max:.4f}")
print(f"Two-tailed t-test bootstrap P value (both tails) = {p_value_bs_shifted_2t_sum:.4f}")
Two-tailed t-test bootstrap P value (conservative) = 0.0046
Two-tailed t-test bootstrap P value (both tails) = 0.0037
Permutation#
The permutation approach, closely related to the permutation test, provides a way to directly simulate the null hypothesis of no difference between two groups. It involves pooling all the data, shuffling the group labels, and then reassigning these shuffled labels to create new “groups”. This process disrupts any inherent structure or relationship between the original groups, effectively simulating a scenario where the groups are indistinguishable.
This method is particularly useful when testing the null hypothesis of identical distributions between the two groups, not just equal means. It’s a more general approach that doesn’t rely on specific distributional assumptions, making it suitable for a wider range of data. While it shares similarities with bootstrapping in terms of resampling, it differs in its focus on simulating the null hypothesis rather than estimating the sampling distribution of a specific statistic. It’s worth noting that the permutation approach, when applied to the difference in means, doesn’t explicitly incorporate the standard errors of the groups, unlike the t-statistic.
To facilitate the permutation test, we’ll define a function that shuffles the original arrays and returns permuted samples. This function will be instrumental in creating datasets with randomly reassigned group labels, allowing us to assess the likelihood of observing our original data under the null hypothesis. For further exploration of permutation and bootstrapping techniques, refer to the advanced biostatistical methods I (BIOS 6618).
def permutation_sample(data1, data2):
"""Generate a permutation sample by combining and shuffling two datasets.
This function concatenates `data1` and `data2`, randomly shuffles the
combined array, and then splits it back into two arrays with the
original sizes of `data1` and `data2`, respectively.
Args:
data1: A one-dimensional array-like object representing the first dataset.
data2: A one-dimensional array-like object representing the second dataset.
Returns:
A tuple containing two NumPy arrays:
- permuted_data1: A shuffled version of `data1`.
- permuted_data2: A shuffled version of `data2`.
"""
# Combine the two datasets into a single array
combined_data = np.concatenate([data1, data2])
# Shuffle the combined data in-place
np.random.shuffle(combined_data)
# Split the shuffled data back into two arrays with original sizes
permuted_data1 = combined_data[:len(data1)]
permuted_data2 = combined_data[len(data1):]
return permuted_data1, permuted_data2
The core concept of the permutation test is to repeatedly shuffle the group labels of the original data, effectively simulating the null hypothesis where there’s no true difference between the groups. For each shuffled dataset, we calculate the mean difference (our test statistic) and create a distribution of these permuted mean differences. We then assess how often these permuted differences are as extreme as, or more extreme than, the observed mean difference in our original data. This proportion represents the P value, indicating the probability of observing such an extreme difference by chance if the null hypothesis were true.
# Set random seed for reproducibility
np.random.seed(111)
# Generate 10,000 bootstrap replicates of the mean difference for each permutation samples
n_replicates = 10**4 - 1
# Initialize an empty array to store the bootstrap mean differences
permuted_mean_diffs = np.zeros(n_replicates)
# Generate bootstrap replicates of the mean difference for each permutation sample
for i in range(n_replicates):
# Generate a new permuted sample
x, y = permutation_sample(old, yng)
# Calculate the mean difference for this permuted sample
permuted_mean_diffs[i] = np.mean(x) - np.mean(y)
# We could also use a list comprehension instead of the loop
# permuted_mean_diffs = np.array([
# np.mean(x) - np.mean(y) for _ in range(n_replicates) for x, y in [permutation_sample(old, yng)]
# ])
# Print the first 10 replicates
print(permuted_mean_diffs[:10])
[ -5.45972222 -6.475 13.73611111 -4.79861111 7.3375
7.40833333 -12. 4.71666667 -15.96666667 -5.50694444]
The core logic for calculating the P value remains consistent between the permutation test and the mean-shifting approach. In both cases, we estimate the P value as the proportion of replicates (permuted mean differences or bootstrapped t-statistics from shifted data) that are as extreme as, or more extreme than, the observed statistic (the original mean difference or t-statistic). The fundamental distinction lies in how the null hypothesis is simulated. The permutation test achieves this by shuffling group labels, while the mean-shifting approach shifts the data in each group to a common mean, effectively assuming no difference between the groups.
# Calculate one-sided P value using the permutation distribution of mean differences
if mean_diff >= 0:
p_value_permutation_up = np.mean(permuted_mean_diffs >= mean_diff)
p_value_permutation_low = np.mean(permuted_mean_diffs <= -mean_diff)
else:
p_value_permutation_low = np.mean(permuted_mean_diffs <= mean_diff)
p_value_permutation_up = np.mean(permuted_mean_diffs >= -mean_diff)
p_value_permutation_1t = p_value_permutation_up if mean_diff >= 0 else p_value_permutation_low
# Print the P value
print(f"One-sided P value obtained using permutation test (mean difference) = {p_value_permutation_1t:.4f}")
One-sided P value obtained using permutation test (mean difference) = 0.0018
# Plot the histogram of the shuffled mean differences
hist, bins, patches = plt.hist(
permuted_mean_diffs,
density=False,
bins=int(n_replicates**.5),
color='gold',
# alpha=0.75,
)
# Annotate the observed mean difference
plt.axvline(
x=mean_diff, # type: ignore
color='limegreen',
linestyle='-.', lw=2,
label=fr'Observed $\bar x - \bar y$ ({mean_diff:.3f})')
# Determine the direction of the observed difference and plot accordingly
if mean_diff >= 0:
# Plot the histogram of the mean differences >= observed mean difference
extreme_diffs = permuted_mean_diffs[permuted_mean_diffs >= mean_diff]
# Change the color of the bars based on the direction parameter
for i, bin_edge in enumerate(bins[:-1]):
if np.any(bin_edge >= extreme_diffs):
patches[i].set_facecolor('lime') # type: ignore
else:
# Plot the histogram of the mean differences <= observed mean difference
extreme_diffs = permuted_mean_diffs[permuted_mean_diffs <= mean_diff]
for i, bin_edge in enumerate(bins[:-1]):
if np.any(bin_edge <= extreme_diffs):
patches[i].set_facecolor('lime') # type: ignore
# Add labels and title
plt.xlabel('Mean difference')
plt.ylabel('Frequency')
plt.title(f"Distribution of permutated mean difference under H0 (B={n_replicates})")
# Create a copy of the original patch for the legend
original_patch = mpatches.Patch(color='gold', label=r'Permuted $\bar x - \bar y$')
# Create a patch for the legend
p_value_patch = mpatches.Patch(color='lime', label=f'One-tailed P ({p_value_permutation_1t:.4f})')
# Add the patches to the legend
plt.legend(handles=[original_patch, plt.gca().lines[0], p_value_patch]); # type: ignore
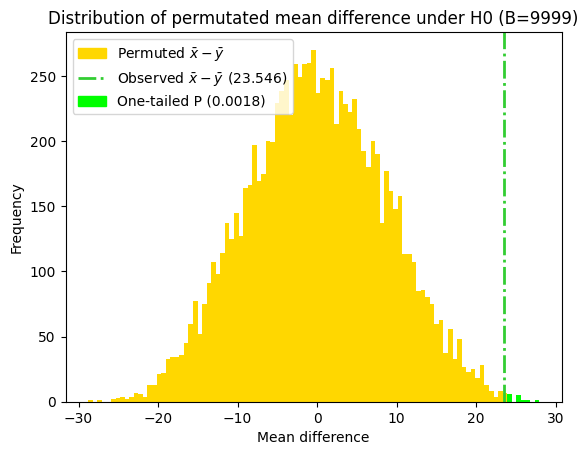
We use the same approach as in the shifting mean mean for computing the two-tailed P value.
# Maximum one-tail
p_value_permut_2t_max = 2 * max(p_value_permutation_low, p_value_permutation_up)
# Sum of the tails
p_value_permut_2t_sum = p_value_permutation_low + p_value_permutation_up
# Print the results
print(f"Two-tailed permutation bootstrap P value (conservative) = {p_value_permut_2t_max:.4f}")
print(f"Two-tailed permutation bootstrap P value (both tails) = {p_value_permut_2t_sum:.4f}")
Two-tailed permutation bootstrap P value (conservative) = 0.0036
Two-tailed permutation bootstrap P value (both tails) = 0.0031
The P values obtained from all the tests we conducted, i.e., permutation test, bootstrapped t-statistic, Mann-Whitney non-parametric approaches, Student’s t-test, and Welch’s t-test, are substantially lower than the conventional significance level of 0.05. This provides compelling evidence to reject the null hypothesis of no difference between the means of the “old” and “young” rat groups. We can confidently assert that a statistically significant difference exists between the two groups, with “young” rats exhibiting, on average, a significantly different (and likely higher) outcome measurement compared to “old” rats.
Interestingly, the permutation test and bootstrapping yielded slightly smaller P values than the parametric t-tests. This might indicate a subtle advantage of these non-parametric methods in detecting the mean difference for this specific dataset. However, all tests consistently lead to the same conclusion: a significant difference exists between the groups.
Navigating the nuances of hypothesis testing involves careful consideration of the null distribution, P value calculation method, and the chosen test statistic. While no single “correct” answer exists, adopting a more conservative approach in P value calculations can help mitigate the risk of type I errors (false positives).
Conclusion#
In this chapter, we explored the unpaired t-test, a fundamental statistical tool for comparing the means of two independent groups. We started by emphasizing the importance of descriptive statistics and visualization in understanding the characteristics of the data before proceeding with hypothesis testing. We then delved into the assumptions underlying the t-test, particularly normality and equal variances, and discussed how to assess and address potential violations of these assumptions.
We examined both the Welch’s t-test (for unequal variances), and standard Student t-test (assuming equal variances), highlighting their formulas, calculations, and interpretations. We also demonstrated how to perform these tests in Python using both the scipy.stats, Pingouin and statsmodels libraries.
Furthermore, we explored the power of bootstrapping and permutation tests as non-parametric alternatives or complements to the traditional t-test. We illustrated how these resampling-based methods can be used to estimate P values and confidence intervals, providing valuable insights even when the underlying assumptions of the t-test might not be fully met.
Finally, we used the penguins dataset to demonstrate the practical application of t-tests and the importance of considering both statistical significance and the visual representation of data. We learned that overlapping distributions do not necessarily imply the absence of a significant difference, especially with small sample sizes.
By mastering the concepts and techniques presented in this chapter, we are now equipped to confidently apply the unpaired t-test in our research and data analysis endeavors, drawing meaningful conclusions about differences between groups and contributing to the advancement of knowledge in the field of life sciences. Remember that the choice between the standard t-test and Welch’s t-test should be guided by a careful assessment of the assumptions and the characteristics of the data. Additionally, consider leveraging the flexibility of bootstrapping and permutation tests when dealing with non-normal data or small sample sizes.
Cheat sheet#
Descriptive statistics and visualization#
# Descriptive statistics
import scipy.stats as stats
stats.describe(data1)
# Box and swarm plots
import matplotlib.pyplot as plt
import seaborn as sns
sns.boxplot(data=[data1, data2])
sns.swarmplot(data=[data1, data2])
Assessing assumptions#
Normality testing#
# Using scipy.stats
# D'Agostino-Pearson K² test
stats.normaltest(data1)
# Shapiro-Wilk
stats.shapiro(data1)
# Using pingouin
import pingouin as pg
pg.normality(data1, method='normaltest')
pg.normality(data1, method='shapiro')
Q-Q plot#
pg.qqplot(data1, dist='norm', confidence=0.95)
Homoscedasticity testing#
# Levene's test for equal variances
stats.levene(data1, data2)
# Bartlett's test for equal variances
stats.bartlett(data1, data2)
# Using pingouin
pg.homoscedasticity([data1, data2], method='levene')
pg.homoscedasticity([data1, data2], method='bartlett')
# Homoscedasticity testing with DataFrame
pg.homoscedasticity(
data=data,
dv=dv,
group=group,
method='levene')
T-test#
Welch’s t-test#
# Using scipy.stats
stats.ttest_ind(data1, data2, equal_var=False)
#t = stats.ttest_ind(x, y, equal_var=False)[0]
# Using pingouin
pg.ttest(data1, data2, correction=True)
Student’s t-test#
# Using scipy.stats
stats.ttest_ind(data1, data2, equal_var=True)
# One-sided t-test
stats.ttest_ind(x - 3,
y,
equal_var=True,
alternative='greater',
nan_policy='omit', # scipy doesn't remove missing values automatically
)
# Using pingouin
pg.ttest(data1, data2, correction=False)
# T-test with a DataFrame
pg.ttest(
x=x, # the method removes missing values by default
y=y,
correction=False)
# One-sided t-test
pg.ttest(
x=x - 3,
y=y,
correction=False,
alternative='greater')
# Using statsmodels API
import statsmodels.api as sm
sm.stats.ttest_ind(
x1=x,
# statsmodels doesn't support policy for missing values
x2=y,
usevar='pooled', # Specify equal variances assumption
alternative='larger', # Test if the Adelie bill depth mean (x1) is larger
value=3 # difference between the means (x1 - x2) under the null hypothesis
)
Effect size#
pg.compute_effsize(x, y, eftype='cohen')
Non-parametric Mann-Whitney U test#
from scipy.stats import mannwhitneyu
# Perform Mann-Whitney U test with exact p-value calculation
mannwhitneyu(x, y, method='exact')
# Perform Mann-Whitney U test with asymptotic (normal approximation) p-value calculation
mannwhitneyu(x, y, method='asymptotic', use_continuity=False)
# Perform Mann-Whitney U test with Pingouin backend
pg.mwu(x, y, method='asymptotic', use_continuity=False, alternative='two-sided')
Bootstrapping and permutation tests#
Bootstrapping#
# Generate B bootstrap replicates of the mean for each group
# !Make sure to choose exactly N elements randomly **with replacement**
n_replicates = 10000
bs_data1_means = np.array([
np.mean(
np.random.choice(
data1,
size=len(data1),
replace=True
)) for _ in range(n_replicates)
])
# bs_data2_means = ...
# Calculate the statistics of interest `bs` for each replicate
bs_m = np.mean(bs_data2_means - bs_data1_means)
bs_s = np.std(bs_data2_means - bs_data1_means, ddof=1)
# Bootstrap percentile confidence interval
np.percentile(bs, [2.5, 97.5])
# 95% normal confidence interval
bs_w = norm.ppf(0.975) * bs_s
(bs_m - bs_w, bs_m + bs_w)
Bootstrapping with pingouin#
bs_ci, bt = pg.compute_bootci(
x=data1,
y=data2,
func=lambda x,y : np.mean(data1) - np.mean(data2),
return_dist=True,)
P value#
Bootstrapped t-statistics of shifted data#
n_replicates = 10**4 - 1 # 99 rule
# Calculate the combined mean of both groups
combined_mean = np.mean(np.concatenate([data1, data2]))
# Shift the data in each group to have the same mean (combined_mean)
data1_shifted = data1 - np.mean(data1) + combined_mean
data2_shifted = data2 - np.mean(data2) + combined_mean
# Generate B bootstrap replicates for each shifted group
bs_shifted_data1 = np.array([
np.random.choice(data1_shifted, size=len(data1), replace=True) for _ in range(n_replicates)])
bs_shifted_data2 = np.array([
np.random.choice(data2_shifted, size=len(data2), replace=True) for _ in range(n_replicates)])
# Calculate Welch's t-statistic for each bootstrap replicate
bs_t = np.array([
stats.ttest_ind(x, y, equal_var=False)[0] for x, y in zip(bs_shifted_data1, bs_shifted_data2)
])
# Calculate P values using bootstrapping, considering the direction of the observed statistic
# 1. Calculate lower and upper tail
if t >= 0:
p_value_bs_t_up = np.mean(bs_t >= t)
p_value_bs_t_low = np.mean(bs_t <= -t)
else:
p_value_bs_t_low = np.mean(bs_t <= t)
p_value_bs_t_up = np.mean(bs_t >= -t)
# 2. Attribute the one-tailed P value
p_value_bs_t_up if t >= 0 else p_value_bs_t_low
# 3. Attribute the two-tailed P values
# Maximum one-tail
2 * max(p_value_bs_t_low, p_value_bs_t_up)
# Sum of the tails
p_value_bs_t_low + p_value_bs_t_up
Permutation#
def permutation_sample(data1, data2):
# Combine the two datasets into a single array
combined_data = np.concatenate([data1, data2])
# Shuffle the combined data in-place
np.random.shuffle(combined_data)
# Split the shuffled data back into two arrays with original sizes
permuted_data1 = combined_data[:len(data1)]
permuted_data2 = combined_data[len(data1):]
return permuted_data1, permuted_data2
permuted_mean_diffs = np.array([
np.mean(x) - np.mean(y) for _ in range(n_replicates) for x, y in [
permutation_sample(data1, data2)]
])
# Calculate permutation P values
if mean_diff >= 0:
p_value_permutation_up = np.mean(permuted_mean_diffs >= mean_diff)
p_value_permutation_low = np.mean(permuted_mean_diffs <= -mean_diff)
else:
p_value_permutation_low = np.mean(permuted_mean_diffs <= mean_diff)
p_value_permutation_up = np.mean(permuted_mean_diffs >= -mean_diff)
# One-tailed P value
p_value_permutation_up if mean_diff >= 0 else p_value_permutation_low
# Two-tailed P values
# Maximum one-tail
2 * max(p_value_permutation_low, p_value_permutation_up)
# Sum of the tails
p_value_permutation_low + p_value_permutation_up
Session Information#
The output below details all packages and version necessary to reproduce the results in this report.
Show code cell source
!python --version
print("-------------")
from importlib.metadata import version
# List of packages we want to check the version
packages = ['numpy', 'pandas', 'matplotlib', 'seaborn', 'scipy', 'pingouin', 'statsmodels']
# Initialize an empty list to store the versions
versions = []
# Loop over the packages
for package in packages:
try:
# Get the version of the package
package_version = version(package)
# Append the version to the list
versions.append(package_version)
except Exception: # Use a more general exception for broader compatibility
versions.append('Not installed')
# Print the versions
for package, version in zip(packages, versions):
print(f'{package}: {version}')
Python 3.12.7
-------------
numpy: 1.26.4
pandas: 2.2.2
matplotlib: 3.9.2
seaborn: 0.13.2
scipy: 1.14.1
pingouin: 0.5.5
statsmodels: 0.14.2
