Comparing paired data#
Introduction#
In hypothesis testing, the paired t-test is an indispensable tool when we need to ascertain if there’s a genuine difference within the same group or individuals, but at two distinct points in time or under two different conditions. This scenario is commonplace in a variety of research contexts, such as evaluating the effectiveness of a training program by comparing participants’ performance before and after the program, or assessing the impact of a new diet on patients’ cholesterol levels by examining their readings before and after adopting the diet. The paired t-test empowers us to glean statistically robust insights from such data, facilitating informed decision-making.
The hallmark of the paired t-test is its focus on paired or matched data. Here, each observation in one group has a corresponding observation in the other group. This pairing could stem from repeated measurements on the same subjects (e.g., before-and-after measurements), or it could involve matching subjects based on relevant characteristics (e.g., age, gender) to minimize confounding factors. The test zeroes in on the differences between these paired observations, gauging whether the average difference is statistically significant or merely attributable to chance.
Before embarking on a paired t-test analysis, it’s imperative to ensure our data aligns with certain assumptions:
Normality: the differences between the paired observations should ideally conform to a normal distribution. However, like its unpaired counterpart, the paired t-test exhibits reasonable resilience to moderate departures from normality, particularly when dealing with larger sample sizes.
Independence: the differences between the paired observations should be independent of each other.
At its core, the paired t-test operates by computing a test statistic (as discussed in details in the chapter on the unpaired t-test) that encapsulates the average difference between the paired observations relative to the variability of these differences. This test statistic adheres to a well-defined distribution (the t-distribution, also covered in a preivous chapter) under the null hypothesis of no difference. By juxtaposing the calculated test statistic with the anticipated distribution, we derive a P value. Should the P value dip below our predetermined significance level (α), we reject the null hypothesis and infer the presence of a statistically significant difference.
In the forthcoming sections, we’ll embark on a deeper exploration of the mathematical underpinnings of the paired t-test, explore its practical applications through illustrative examples, and equip ourselves with the knowledge and confidence to wield this test effectively in your own analytical endeavors.
Preparing data for hypothesis testing#
Descriptive statistics#
In this section, we will introduce the importance of descriptive statistics and visualization in understanding the characteristics of the paired data being compared. We will emphasize how these techniques provide valuable insights into the central tendency, spread, and distribution of the differences between the paired observations, which are crucial for interpreting the results of the paired t-test.
Fisher analyzed an experiment conducted by Charles Darwin, where the growth of plants originating from self-fertilized seeds was compared to those from cross-fertilized seeds. To ensure fairness, Darwin planted these seeds in pairs, side-by-side, effectively controlling for any environmental factors (like soil quality, temperature, or sunlight) that might influence both types of seeds. The data below showcases one such matched set.
# We use the data from Table 31.1 (page 307) of the book Intuitive Biostatistics 4th Edition
import numpy as np
import pandas as pd
# Import the raw data as Series; unit is inches
crossed_fertil = pd.Series(
[23.5, 12, 21, 22, 19.125, 21.5, 22.125, 20.375, 18.250, 21.625, 23.250, 21, 22.125, 23, 12])
self_fertil = pd.Series(
[17.375, 20.375, 20, 20, 18.375, 18.625, 18.625, 15.25, 16.5, 18, 16.25, 18, 12.75, 15.5, 18])
# note that each row represents a paired observation
# Concatenate the data in a DataFrame for some operations
data_fert = pd.concat(
[crossed_fertil, self_fertil],
keys=['crossed_fertil', 'self_fertil'],
axis=1)
Performing descriptive statistics and visualization is just as crucial in the context of a paired t-test as it is in unpaired tests. However, we need to adapt our approach to focus on the differences between the paired observations, as these differences form the core of the paired t-test analysis.
Utilizing a dictionary or a DataFrame enhances the clarity of the data structure and simplifies subsequent analysis and visualization.
# Calculate the difference between cross-fertilization and self-fertilization for each pair
#differences_fert = data_fert['crossed_fertil'] - data_fert['self_fertil']
differences_fert = crossed_fertil - self_fertil
# Print or display the calculated differences
print(differences_fert)
0 6.125
1 -8.375
2 1.000
3 2.000
4 0.750
5 2.875
6 3.500
7 5.125
8 1.750
9 3.625
10 7.000
11 3.000
12 9.375
13 7.500
14 -6.000
dtype: float64
import scipy.stats as stats
# Descriptive statistics of the differences
differences_fert_stats = stats.describe(differences_fert)
print("Descriptive statistics for the differences:\n", differences_fert_stats)
Descriptive statistics for the differences:
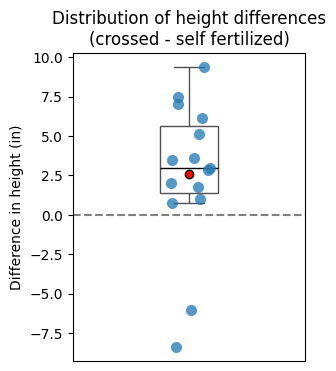
DescribeResult(nobs=15, minmax=(-8.375, 9.375), mean=2.6166666666666667, variance=22.259970238095235, skewness=-0.9920929151820244, kurtosis=0.6057395436698894)
Data visualization#
In paired data analysis, visualizing the differences between the paired values is crucial for gaining insights into the data and assessing the assumptions of the paired t-test. These visualizations help us understand the magnitude and direction of the changes, identify potential outliers, and check if the differences follow a roughly normal distribution. Common visualization techniques for paired data differences include:
Boxplots: provide a compact summary of the distribution of the differences, including median, quartiles, and potential outliers.
Before-after plots: show how each individual pair’s values change, highlighting overall trends and individual variations.
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(3,4))
# Create the stripplot
sns.stripplot(
y=differences_fert,
size=8,
alpha=0.75)
# Add a boxplot on the right side
sns.boxplot(
y=differences_fert,
width=0.25,
showmeans=True, # Show mean as a point inside the boxplot
fliersize=0, # Hide outliers from boxplot to avoid visual clutter
# Custumize a few elements of the plot
boxprops={'facecolor': 'none'}, # Make the boxplot transparent
medianprops={'color': 'black'},
meanprops={'marker': 'o', 'markerfacecolor': 'red', 'markeredgecolor': 'black'},
)
# Add a horizontal line at y=0 (no difference)
plt.axhline(
y=0,
color='gray',
linestyle='--',
linewidth=1.5)
# Set plot labels and title
plt.ylabel('Difference in height (in)')
plt.xticks([])
plt.title('Distribution of height differences\n(crossed - self fertilized)');
import pingouin as pg
pd.set_option('future.no_silent_downcasting', True)
plt.figure(figsize=(4, 4.5))
pg.plot_paired(
# We need to reshape the DataFrame in the long format
data=data_fert.reset_index().melt(
value_vars=['crossed_fertil', 'self_fertil'],
id_vars='index',
var_name='fertilization',
value_name='plant_height'),
dv='plant_height',
within='fertilization',
subject='index',
boxplot=True,
orient='v',
# boxplot_in_front=False, # fix submitted via a PR
boxplot_kwargs={'color': 'white', 'linewidth': 2, 'zorder': 1},
)
plt.xlabel(None) # type: ignore
plt.ylabel("Plant height (in)")
sns.despine(trim=True); # not default in Pingouin anymore
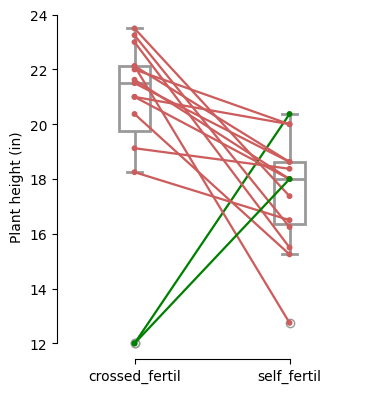
The lines connecting the pairs of data points are color-coded to highlight changes: green indicates an increase, indianred a decrease, and grey signifies no change between the two measurements.
Assessing assumptions#
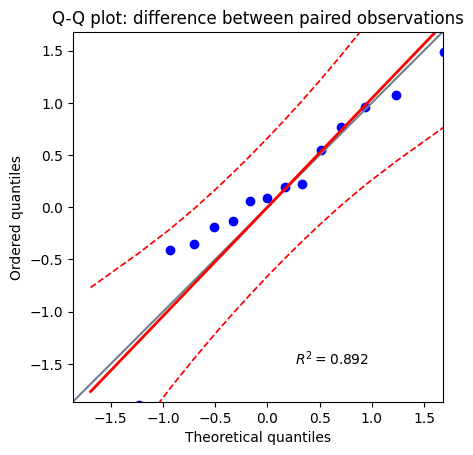
Before proceeding with any hypothesis test, it’s crucial to verify that our data adheres to the underlying assumptions of the chosen statistical method. This subsection emphasizes the importance of checking for normality, a common assumption in many parametric tests, including the paired t-test. We’ll briefly discuss the methods used to assess this assumption, such as normality tests and visual inspections of histograms or Q-Q plots, as discussed in greater details in the chapter about normality test. These tests help us gauge whether the observed differences between paired observations align with the expected characteristics of a normal distribution.
Normality testing#
One of the fundamental assumptions of the paired t-test is that the differences between the paired observations are approximately normally distributed. To assess this assumption, we employ normality tests such as the D’Agostino-Pearson omnibus K² and Shapiro-Wilk tests, or visual inspections of histograms or Q-Q plots. These tests help us gauge whether the observed differences align with the expected characteristics of a normal distribution.
# D'Agostino-Pearson K² test
k2_diff, pval_k2_diff = stats.normaltest(differences_fert)
print(f"Differences between paired observations\tD'Agostino-Pearson omnibus:\n\
K2={k2_diff:.2f}, P value={pval_k2_diff:.3f}")
# Shapiro-Wilk
shapiro_diff, pval_shapiro_diff = stats.shapiro(differences_fert)
print(f"Differences between paired observations\tShapiro-Wilk's normality test:\n\
P value={pval_shapiro_diff:.3f}")
# Interpret the results
alpha = 0.05 # Set the desired significance level
if pval_k2_diff > alpha or pval_shapiro_diff > alpha:
print("\nThe differences are not inconsistent with a normal distribution\n\
(failed to reject null hypothesis of normality)")
else:
print("\nThe differences are not consistent with a normal distribution")
Differences between paired observations D'Agostino-Pearson omnibus:
K2=5.21, P value=0.074
Differences between paired observations Shapiro-Wilk's normality test:
P value=0.098
The differences are not inconsistent with a normal distribution
(failed to reject null hypothesis of normality)
c:\Users\Sébastien\Documents\data_science\biostatistics\intuitive_biostatistics\.env\Lib\site-packages\scipy\stats\_axis_nan_policy.py:418: UserWarning: `kurtosistest` p-value may be inaccurate with fewer than 20 observations; only n=15 observations were given.
return hypotest_fun_in(*args, **kwds)
Similar to our approach in unpaired t-tests, we can utilize the pingouin library for normality testing and Q-Q plotting in the context of paired t-tests, directly on the dataframe.
# Function to perform tests and print results
def normality_tests(data, sample_type):
s = f"{'Test':<20} {'W':<6} {'P value':<8} {'normal'}"
print(f"Normality tests for {sample_type}".center(len(s), "-"))
print(s)
# D'Agostino-Pearson Test
dagostino_results = pg.normality(
data,
method='normaltest')
print(f"{'D\'Agostino-Pearson':<20} {dagostino_results.loc[0, 'W']:<6.2f} \
{dagostino_results['pval'][0]:<8.3f} {dagostino_results.loc[0, 'normal']}")
# Shapiro-Wilk Test
shapiro_results = pg.normality(
data,
method='shapiro')
print(f"{'Shapiro-Wilk':<20} {shapiro_results.loc[0, 'W']:<6.2f} \
{shapiro_results['pval'][0]:<8.3f} {shapiro_results.loc[0, 'normal']}")
print("-" * len(s))
# Perform tests and print results
normality_tests(differences_fert, "difference between paired observations")
Normality tests for difference between paired observations
Test W P value normal
D'Agostino-Pearson 5.21 0.074 True
Shapiro-Wilk 0.90 0.098 True
-------------------------------------------
# Plotting Q-Q plot
pg.qqplot(
differences_fert,
dist='norm',
confidence=0.95,)
plt.title("Q-Q plot: difference between paired observations");
While the paired t-test is also reasonably robust to moderate deviations from normality in the differences between paired observations, especially with larger sample sizes, severe violations can impact the accuracy of the test’s results. When the normality assumption is not met for the differences, the calculated P value may be unreliable, potentially leading to incorrect conclusions about the statistical significance of the mean difference.
In such cases, we have a few options:
Transform the differences: if the differences exhibit a clear pattern of non-normality, we might attempt to transform them to achieve a more normal distribution.
Use a non-parametric alternative: when transformations are ineffective or impractical, we can consider a non-parametric test like the Wilcoxon signed-rank test (discussed in a later section), which does not rely on the normality assumption for the differences.
Proceed with caution: if the sample size is relatively large and the deviations from normality in the differences are not severe, we might proceed with the paired t-test, acknowledging the potential limitations in the interpretation of the results.
Note on homoscedasticity#
The assumption of homoscedasticity, or equal variances, is crucial for the unpaired t-test, but it is not a requirement for the paired t-test.
The paired t-test focuses on the differences between paired observations. It inherently assumes that these differences have a constant variance. There’s no need to test for equal variances between the two original groups, as the test operates on a single set of differences.
Assessing the significance of paired difference mean with t-test#
The central question in many research studies involving paired data is whether an intervention, treatment, or the passage of time leads to a meaningful change within the same group or individuals. In this section, we’ll explore how the paired t-test enables us to answer this question by comparing the means of paired observations, effectively assessing the significance of the average change or difference.
The t-ratio#
At the core of the paired t-test also lies the t-ratio (or t-value, or t-score), and abbreviated t, a key statistic that quantifies the magnitude of the average difference between paired observations relative to the variability of those differences. The t-ratio used in the paired t-test shares a conceptual resemblance to both the t-statistic used in confidence intervals for a single mean and the t-ratio used in the unpaired t-test. All three involve a ratio of a difference (or an estimated parameter) to a measure of variability, and they follow a t-distribution. However, the t-ratio in the paired t-test specifically focuses on assessing the mean difference within the same group or individuals under different conditions, while the t-statistic for confidence intervals estimates a single population mean, and the t-ratio in the unpaired t-test compares the means of two independent groups.
Manual calculation#
In this subsection, we’ll delve into the mathematical underpinnings of the t-ratio in the context of the paired t-test, exploring how it incorporates the mean difference, the standard deviation of the differences, and the sample size to provide a standardized measure of the effect. Understanding the t-ratio is crucial for interpreting the results of the paired t-test and drawing meaningful conclusions about the statistical significance of any observed changes within the paired data.
In the paired t-test, we don’t need to worry about unequal variances between two separate groups. Instead, we focus on the variance of the differences between the paired observations.
The t-ratio for the paired t-test is calculated as follows:
where:
\(\overline{D}\) is the mean of the differences between the paired observations \(D_i = X_{1i} - X_{2i}\)
\(s_D^2\) is the variance of the differences
\(n\) is the number of pairs (or the sample size)
The standard error of the mean difference, denoted by \(s_{\overline{D}}\), is calculated as:
This standard error quantifies the uncertainty in our estimate of the mean difference.
We can then express the t-ratio as:
The degrees of freedom for this t-statistic are simply:
where \(n\) is the number of pairs.
# Calculate the standard error of the mean difference with se²=s²/n
se_diff = (differences_fert_stats.variance / differences_fert_stats.nobs)**.5
# Calculate the t-statistic for the paired t-test
t_statistic_paired = differences_fert_stats.mean / se_diff
# Calculate the degrees of freedom
df_paired = differences_fert_stats.nobs - 1
# Print the results
print(f"t-statistic (paired) = {t_statistic_paired:.5f} with {df_paired} degrees of freedom")
t-statistic (paired) = 2.14799 with 14 degrees of freedom
P value#
Now that we have our t-statistic and degrees of freedom, we can determine the P value associated with our test, as well as construct a confidence interval for the true mean difference in the population. The P value will quantify the probability of observing a t-statistic as extreme as (or more extreme than) the one we calculated, assuming the null hypothesis of no difference between the paired observations is true. We will utilize the cumulative distribution function (CDF) of the t-distribution to compute this probability. The confidence interval will provide a range of plausible values for the true mean difference, giving us a sense of the magnitude of the effect and the uncertainty associated with our estimate.
# Calculate the P value using the t-distribution (two-sided test)
p_value_paired = 2 * (1 - stats.t.cdf(abs(t_statistic_paired), df_paired))
# Print the results
print(f"P value for the paired t-test = {p_value_paired:.5f}")
P value for the paired t-test = 0.04970
Visualizing the test results#
To gain a deeper understanding of the results of the paired t-test, let’s visualize the t-statistic, the critical t-values that define the rejection regions, and the areas under the t-distribution corresponding to the P value. This visual representation will help us grasp the statistical significance of the observed mean difference and the role of the degrees of freedom in shaping the t-distribution.
# Significance level (alpha)
α = 0.05
# Calculate critical t-values (two-tailed test)
t_crit_lower = stats.t.ppf(α/2, df_paired)
t_crit_upper = stats.t.ppf(1 - α/2, df_paired)
# Generate x values for plotting
x = np.linspace(-5, 5, 1000)
hx = stats.t.pdf(x, df_paired)
# Create the plot
plt.plot(x, hx, lw=2, color="black")
# Plot the critical t-values
plt.axvline(
x=t_crit_lower, # type: ignore
color='orangered',
linestyle='--')
plt.axvline(
x=t_crit_upper, # type: ignore
color='orangered',
linestyle='--',
label=f't* ({t_crit_upper:.3f})')
# Shade the rejection regions (alpha)
plt.fill_between(
x[x <= t_crit_lower],
hx[x <= t_crit_lower],
linestyle="-",
linewidth=2,
color='tomato',
label=f'α ({α})')
plt.fill_between(
x[x >= t_crit_upper],
hx[x >= t_crit_upper],
linestyle="-",
linewidth=2,
color='tomato')
# Plot the observed t-statistic
plt.axvline(
x=t_statistic_paired,
color='limegreen',
linestyle='-.',
label=f't ({t_statistic_paired:.3f})')
# Shade the P-value areas (two-tailed)
plt.fill_between(
x[x <= -abs(t_statistic_paired)],
hx[x <= -abs(t_statistic_paired)],
color='greenyellow',
label=f'P ({p_value_paired:.4f})')
plt.fill_between(
x[x >= abs(t_statistic_paired)],
hx[x >= abs(t_statistic_paired)],
color='greenyellow')
# Add labels and title
plt.xlabel('t')
plt.ylabel('Density')
plt.margins(x=0.05, y=0)
plt.yticks([])
plt.title(f"t-distribution (DF={df_paired}) | Paired t-test, two-tailed")
plt.legend();
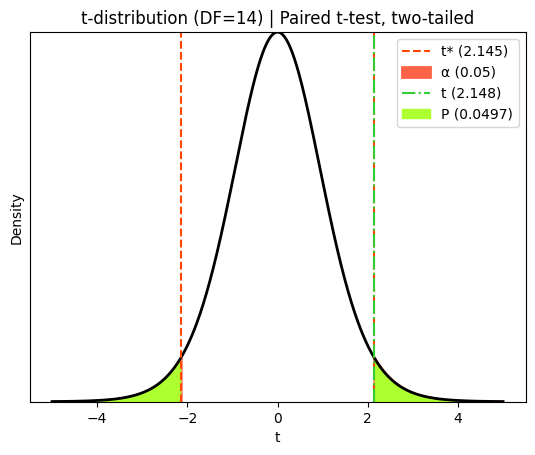
The red dashed lines in this diagram represent the critical t-values that define the rejection regions for a two-tailed paired t-test at a 5% significance level. The ‘tails’ of the curve outside these lines each represent 2.5% of the probability distribution under the null hypothesis (that the true population mean difference is zero).
The green dot-dashed line represents the observed t-statistic calculated from our sample data. The P value corresponds to the total probability of observing a t-statistic as extreme as (or more extreme than) the one we calculated, assuming the null hypothesis is true. In a two-tailed test like this, we consider both tails of the distribution because the true population mean difference could be either higher or lower than zero. One-tailed tests are used when we have a directional hypothesis, specifically testing if the difference is ‘less than zero’ or ‘greater than zero’.
Confidence interval#
A confidence interval provides a range of plausible values for the true difference in population means when comparing two paired groups. It gives us an idea of the precision of our estimate of this difference.
Since we’re dealing with paired data, we’ll use the differences between the paired observations to calculate the confidence interval. Here’s how it’s done:
Calculate the differences: for each pair of observations, calculate the difference \(D_i = X_{1i} - X_{2i}\)
Calculate the mean difference: calculate the mean of these differences \(\overline{D}\). This is the point estimate of the true difference in population means
Calculate the standard deviation of the differences: calculate the standard deviation of the differences \(s_D\)
Calculate the standard error: the standard error of the mean difference for paired data is calculated as \(s_D / \sqrt{n}\), where \(n\) is the number of pairs
Determine the degrees of freedom: the degrees of freedom for a paired t-test are \(n - 1\)
Find the critical t-value: using the desired confidence level (e.g., 95%) and the calculated degrees of freedom, find the corresponding t* from the t-distribution table
Calculate the margin of error (\(W\)): multiply the standard error by the critical t-value
Construct the confidence interval: subtract and add the margin of error to the mean difference to obtain the lower and upper bounds of the confidence interval: \(\overline{D} \pm W\)
# Calculate the confidence interval (e.g., 95% confidence)
confidence_level = 0.95
margin_of_error_paired = stats.t.ppf((1 + confidence_level) / 2, df_paired) * se_diff
ci_paired = (
differences_fert_stats.mean - margin_of_error_paired,
differences_fert_stats.mean + margin_of_error_paired)
# Print the results
print(f"Paired difference mean (crossed - self) = {differences_fert_stats.mean:.3f}")
print(f"95% confidence interval for the mean difference: \
[{ci_paired[0]:.3f}, {ci_paired[1]:.3f}]")
Paired difference mean (crossed - self) = 2.617
95% confidence interval for the mean difference: [0.004, 5.229]
Performing the paired t-test in Python#
Let’s conduct the paired t-test using both the scipy.stats and pingouin libraries in Python. We’ll compare their implementations and outputs, highlighting their respective advantages.
# Paired t-test using SciPy looking at the \bar{x} - \bar{y} difference
t_statistic_scipy_paired, p_value_scipy_paired = stats.ttest_rel(crossed_fertil, self_fertil)
# Paired t-test using Pingouin looking at the \bar{x} - \bar{y} difference
ttest_results_pingouin_paired = pg.ttest(x=crossed_fertil, y=self_fertil, paired=True)
# Print the results
print("Paired t-test results (SciPy):")
print(f"t-statistic = {t_statistic_scipy_paired:.3f}, P value = {p_value_scipy_paired:.4f}")
print("\nPaired t-test results (Pingouin):")
ttest_results_pingouin_paired
Paired t-test results (SciPy):
t-statistic = 2.148, P value = 0.0497
Paired t-test results (Pingouin):
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 2.147987 | 14 | two-sided | 0.049703 | [0.0, 5.23] | 0.889908 | 1.544 | 0.892939 |
The paired t-test yielded a t-statistic of 2.148 with an associated P value of 0.0497. This P value is slightly less than the commonly used significance level of 0.05, suggesting evidence to reject the null hypothesis of no difference between the paired measurements. Therefore, we conclude that there is a statistically significant difference in the measurements before and after the intervention (or between the paired conditions).
Furthermore, the 95% confidence interval for the mean difference is [0.004, 5.229]. This suggests that we can be 95% confident that the true population mean difference lies within this range. The fact that this interval does not include zero further supports the conclusion that there is a significant difference between the paired measurements.
Follow-up analyses#
To gain a deeper understanding of the observed effect beyond statistical significance, we’ll conduct some follow-up analyses. This will involve examining the effect size to quantify the magnitude of the difference and assessing the effectiveness of the pairing strategy employed in the experimental design.
Effect size#
While the P value from the paired t-test informs us about the statistical significance of the observed mean difference, it doesn’t reveal the magnitude of this difference. To gain a more comprehensive understanding of the effect, we turn to effect size measures. These statistics quantify the size of the effect in a standardized way, allowing us to gauge its practical significance and compare it across different studies or contexts.
In the context of paired t-tests, a common effect size measure is Cohen’s \(d\). It expresses the mean difference in terms of standard deviation units, providing a scale-free measure of the effect’s size. We have previously encountered the effect size statistics in the chapter on statistical power and sample size, notably in the case of comparison of two groups.
While the general idea of effect size remains the same, the specific calculation of Cohen’s d for paired t-tests differs slightly, as it focuses on the standard deviation of the differences (\(s_D\)) between paired observations rather than the pooled standard deviation of two independent groups:
where:
\(\overline{D}\) represents the mean of the differences between the paired observations
\(s_D\) represents the standard deviation of the differences
# Calculate Cohen's d manually for the paired t-test
cohens_d_manual_paired = differences_fert.mean() / differences_fert.std(ddof=1)
print(f"Cohen's d (manual, paired): {cohens_d_manual_paired:.3f}")
Cohen's d (manual, paired): 0.555
Conveniently, many statistical libraries automatically report Cohen’s \(d\) alongside the results of the paired t-test, for example compute_effsize function provided by the Pingouin library. Note that Pingouin applies a bias correction to Cohen’s \(d\), especially for smaller sample sizes. This correction adjusts for the fact that the sample standard deviation tends to slightly underestimate the population standard deviation. Your manual calculation might not include this correction.
# Calculate unbiased Cohen's d using pingouin for paired t-test
effect_size_pingouin_paired = pg.compute_effsize(crossed_fertil, self_fertil, paired=True, eftype='Cohen')
print(f"Unbiased Cohen's d (pingouin, paired): {effect_size_pingouin_paired:.3f}")
Unbiased Cohen's d (pingouin, paired): 0.890
The conventional interpretation of Cohen’s d for paired t-tests aligns with the general guidelines:
Small effect: d ≈ 0.2
Medium effect: d ≈ 0.5
Large effect: d ≈ 0.8
In the current example, the large Cohen’s \(d\) of 0.89 suggests a substantial difference between the two conditions. Encountering a high P value (0.0497) with a large effect size suggests that while there might be a substantial effect present, the study lacks sufficient power to confidently detect it due to the small sample size. This underscores the importance of considering both P values and effect sizes when interpreting research findings and highlights the need for adequate sample sizes to draw reliable conclusions.
Evaluating the effectiveness of pairing#
The paired t-test derives its power from the inherent connection or correlation between paired observations. This correlation, often arising from repeated measures on the same subjects or careful matching of pairs, allows the test to focus on the differences between the pairs, effectively reducing variability and increasing the sensitivity to detect true effects.
However, the success of the paired t-test hinges on the strength of this correlation. Ideally, when designing an experiment with paired samples, we aim for a strong positive correlation between the paired measurements, i.e., when one measurement in a pair increases, the other measurement also tends to increase (or if one decreases, the other also tends to decrease). This indicates that the pairing or matching process has been effective in controlling for extraneous factors and isolating the effect of interest.
In contrast, if the correlation between the paired observations is weak or absent, the paired t-test might not offer any advantage over an unpaired t-test. In fact, in some cases, the paired t-test might even have lower power due to the loss of degrees of freedom associated with the pairing.
# Calculate the Pearson correlation coefficient
pearson_r = np.corrcoef(crossed_fertil, self_fertil)[0, 1]
# Create the scatterplot with regression line
ax = sns.regplot(
x=crossed_fertil,
y=self_fertil,
line_kws={'label':f'Pearson r = {pearson_r:.3f}'},
)
# Make the axes aspect ratio equal (square)
ax.set_aspect('equal')
# Set plot labels and title
plt.title('Testing the effectiveness of pairing')
plt.xlabel('Cross-fertilized plant height (in)')
plt.ylabel('Self-fertilized plant height (in)')
# Adjust plot limits for better visual clarity
plt.xlim(10, 25)
plt.ylim(10, 25) # Ensure both axes have the same limits for easier comparison
# Add a legend with no frame
plt.legend(frameon=False);
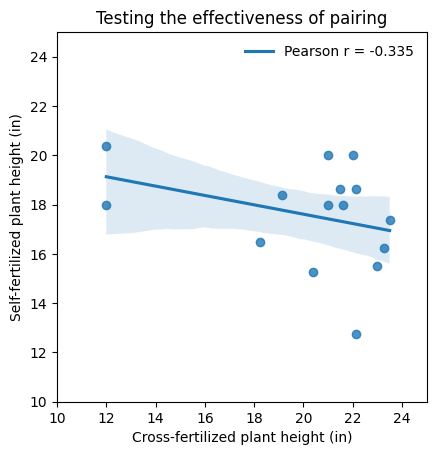
In this dataset, the weak or absent correlation between paired observations suggests ineffective pairing, leading to high variability in the differences. This increased variability can obscure true effects, potentially resulting in a higher P value even when a substantial difference exists. Consequently, we might observe a large effect size (Cohen’s d) but fail to achieve statistical significance due to the limited sample size and the noise introduced by ineffective pairing.
The current scenario, i.e., a high P value coupled with a large effect size, is more likely to occur when the pairing strategy is suboptimal. The large effect size hints at a meaningful difference, but the high variability arising from ineffective pairing hinders our ability to confidently detect it, especially with a small sample.
Extensions of the paired t-test#
One-sided t-test#
In the context of cross-fertilization compared to self-fertilization, looking at the height variable, we can perform a one-sided paired t-test to investigate if cross-fertilization leads to a significant increase in plant height compared to self-fertilization.
Hypothesis:
Null hypothesis (H0): the mean difference in height between cross-fertilized and self-fertilized plants is less than or equal to zero.
Alternative hypothesis (H1): the mean difference in height between cross-fertilized and self-fertilized plants is greater than zero.
We choose a one-sided test because we have a specific directional hypothesis: we expect cross-fertilization to lead to increased height. We are not interested in the possibility that cross-fertilization might lead to a decrease in height.
pg.ttest(crossed_fertil, self_fertil, paired=True, alternative='greater')
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 2.147987 | 14 | greater | 0.024851 | [0.47, inf] | 0.889908 | 3.088 | 0.948282 |
The data suggests that cross-fertilization likely leads to taller plants than self-fertilization, and this difference is not just due to random chance.
Ratio paired t-test#
In some cases, we might be interested in comparing not just the absolute differences between paired observations, but also the proportional or relative changes. This is where the ratio paired t-test comes in. Instead of analyzing the differences directly, this test focuses on the ratios between the paired values.
This approach is particularly useful when:
The magnitude of the change is expected to be related to the baseline value. For example, a 5% increase in heart rate might be more meaningful for someone with a low baseline heart rate than for someone with a high baseline heart rate.
The data are measured on a ratio scale, where a zero value represents a true absence of the quantity being measured. Examples include weight, height, or concentration levels.
The ratio paired t-test essentially performs a paired t-test on the logarithms of the ratios between the paired observations. This transformation allows us to analyze the proportional changes while still leveraging the benefits of the paired t-test framework.
Consider a real-world scenario from Table 31.3 (page 312) of “Intuitive Biostatistics 4th Edition.” This example examines if a drug can boost enzyme activity in cultured cells. Five distinct cell clones were used, with both control (untreated) and treated cells tested in parallel for each clone. This paired design helps account for any natural differences between the cell clones themselves.
# Data
control = np.array([24, 6, 16, 5, 2])
treated = np.array([52, 11, 28, 8, 4])
# Create a DataFrame for Pingouin's plot_paired function
df = pd.DataFrame({'control': control, 'treated': treated})
# Add a 'subject' column to identify each pair
df['subject'] = range(1, len(control) + 1)
# Reshape the data into long format using `pd.melt()`
df_long = df.melt(id_vars='subject', var_name='condition', value_name='enzyme_activity')
# Create the figure with two subplots
fig, axes = plt.subplots(1, 2)
# Left subplot: Before-After plot with original data
pg.plot_paired(
data=df_long,
dv="enzyme_activity",
within="condition",
subject="subject",
boxplot_kwargs={'color': 'white', 'linewidth': 2, 'zorder': 1},
ax=axes[0])
axes[0].set_title('original data')
axes[0].set_ylabel('Enzyme activity')
axes[0].set_xlabel('')
# Right subplot: Before-After plot with log-transformed data
# Apply log transformation to the 'enzyme_activity' column
df_long['log_enzyme_activity'] = np.log(df_long['enzyme_activity'])
pg.plot_paired(
data=df_long,
dv="log_enzyme_activity",
within="condition",
subject="subject",
boxplot_kwargs={'color': 'white', 'linewidth': 2, 'zorder': 1},
ax=axes[1])
axes[1].set_title('log-transformed data')
axes[1].set_ylabel(r'Enzyme activity ($\log$)')
axes[1].set_xlabel('')
plt.suptitle("Before-after plots")
# Adjust layout
plt.tight_layout()
sns.despine(trim=True); # not default in Pingouin anymore
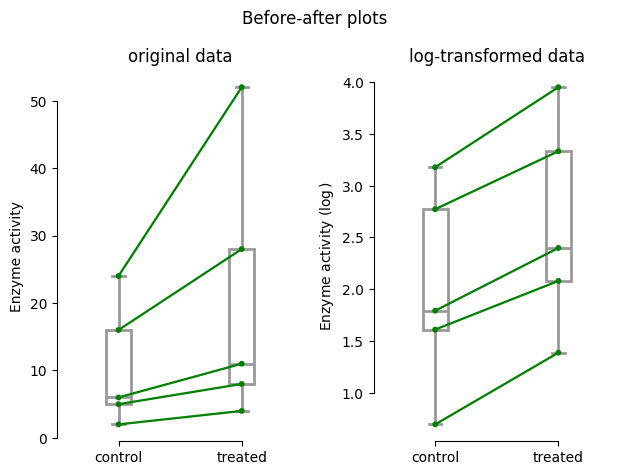
A visual comparison of the before-after plots reveals a stark difference between the original and log-transformed data. In the original scale, the data points appear somewhat scattered, with the changes between control and treated conditions varying considerably depending on the baseline enzyme activity. This heterogeneity in the changes hints at a potential deviation from normality, which could impact the validity of a standard paired t-test.
However, when we examine the log-transformed data, a striking pattern emerges. The lines connecting the paired observations now exhibit a remarkably consistent slope, suggesting a proportional change in enzyme activity across different baseline levels. This visual observation aligns with the assumption of the ratio paired t-test, where we expect the changes to be proportional rather than absolute. Furthermore, the log transformation often helps normalize data, potentially making the ratio paired t-test a more suitable approach for this dataset.
# Perform the paired t-test on the log-transformed data
# Remember we are analyzing \bar{x} - \bar{y}
ttest_results_paired = pg.ttest(
x=np.log10(treated),
y=np.log10(control),
paired=True,
confidence=.95)
ttest_results_paired
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 11.81437 | 4 | two-sided | 0.000294 | [0.21, 0.33] | 0.619234 | 92.646 | 0.189218 |
This extremely low P value indicates strong evidence against the null hypothesis. In other words, we can confidently reject the idea that there is no difference in the log-transformed enzyme activity between the control and treated groups.
Moreover, the high positive t-value suggests a substantial difference between the log-transformed means. The positive sign indicates that the mean of the log-transformed treated group is significantly higher than the mean of the log-transformed control group.
Since we performed the t-test on log-transformed data, we need to interpret the results in terms of ratios or multiplicative changes rather than absolute differences.
# Extract the mean difference and confidence interval from the Pingouin results
mean_diff_log = np.mean(np.log10(treated) - np.log10(control)) # Mean difference on the log scale
ci_log = ttest_results_paired.loc['T-test', 'CI95%'] # 95% CI on the log scale
# Calculate the mean ratio and its confidence interval on the original scale
factor = 10 ** mean_diff_log
ci_original = (10 ** ci_log[0], 10 ** ci_log[1])
# Print the results
print(f"On average, the treatment multiplies enzyme activity by {factor:.3f}, \
with 95% CI from {ci_original[0]:.2f} to {ci_original[1]:.2f}")
On average, the treatment multiplies enzyme activity by 1.860, with 95% CI from 1.62 to 2.14
A ratio of 1.86 signifies that the treated group’s enzyme activity is, on average, 1.86 times the activity in the control group. This translates to an (1.86 - 1) * 100 = 86% increase.
Furthermore, the confidence interval (1.62, 2.14) provides a range of plausible values for the true population mean ratio. Importantly, it doesn’t contain 1.0. Since a ratio of 1.0 would indicate no effect (treated and control groups being the same), the absence of 1.0 in the confidence interval strengthens the conclusion that the observed increase is statistically significant and unlikely due to chance.
McNemar’s test#
McNemar’s test, occasionally referred to as the “within-subjects chi-squared test,” is specifically designed to analyze paired data when the outcome is dichotomous or binary, meaning there are only two possible categories (e.g., yes/no, success/failure). It’s particularly useful for assessing changes in responses or preferences within the same individuals or matched pairs over time or under different conditions.
The McNemar test utilizes a 2x2 table to summarize paired data with a binary outcome. The following table represents the possible outcomes:
Outcome 2: positive |
Outcome 2: negative |
|
|---|---|---|
Outcome 1: positive |
a |
b |
Outcome 1: negative |
c |
d |
where:
“Outcome 1” and “Outcome 2” represent the two measurement points or conditions being compared (e.g., before and after treatment, control vs. experimental group).
“Positive” and “Negative” represent the two possible outcomes for each measurement (e.g., success/failure, presence/absence).
The cells ‘a’, ‘b’, ‘c’, and ‘d’ represent the counts of pairs falling into each combination of outcomes.
McNemar’s test focuses on the discordant pairs (‘b’ and ‘c’), where the outcome changed between the two measurements. These pairs are crucial for assessing whether there’s a statistically significant difference in the proportions of positive outcomes between the two conditions.
The McNemar’s test statistic, often denoted as χ² or sometimes Q, is calculated as \(\chi^2 = \frac{(| b - c | - \mathrm{correction})^2}{b + c}\), where \(b\) and \(c\) represent the counts of discordant pairs, and \(\mathrm{correction}\) is Yates’s continuity correction, typically set to 0.5 or 1 depending on the software. The McNemar’s test statistic, under the null hypothesis, approximately follows a chi-squared distribution with one degree of freedom. However, this approximation can be less accurate for smaller sample sizes. Yates’ continuity correction is applied to improve the accuracy of this approximation by adjusting the calculated chi-squared value slightly downwards. This adjustment helps prevent the overestimation of statistical significance (i.e., finding a significant result when there isn’t one) when dealing with smaller sample sizes or low expected frequencies in the contingency table.
Let’s examine a case-control study exploring the connection between a risk factor (for instance, smoking) and a disease (like lung cancer). Data is gathered in pairs: each person with the disease (a “case”) is paired with someone without it (a “control”), ensuring they’re similar in age, gender, etc. The researchers examined a total of 134 cases and their corresponding controls, and the outcomes are summarized in the following table.
Cases (Risk+) |
Cases (Risk-) |
|
|---|---|---|
Controls (Risk+) |
13 |
4 |
Controls (Risk-) |
25 |
92 |
The table shows the number of pairs falling into each combination of exposure status (risk factor present or absent) for cases and controls.
The 13 pairs where both cases and controls were exposed to the risk factor, as well as the 92 pairs where neither was exposed, provide no information about the association between the risk factor and the disease. These are the concordant pairs.
The remaining pairs (4 and 25) are the discordant pairs, where the case and control have different exposure statuses. These pairs are crucial for assessing the association.
This isn’t exactly a contingency table in the traditional sense. The actual contingency table would look like this:
Risk Factor + |
Risk Factor - |
Total |
|
|---|---|---|---|
Case |
38 |
96 |
134 |
Control |
17 |
117 |
134 |
Total |
55 |
213 |
268 |
McNemar’s test focuses on these discordant pairs to determine if there’s a statistically significant difference in the proportions of cases and controls exposed to the risk factor.
table = np.array(
[
[13, 4],
[25, 92]
]
)
# Extract discordant pair counts from the contingency table
b = table[0, 1] # Count of cases exposed, controls not exposed
c = table[1, 0] # Count of cases not exposed, controls exposed
# Calculate the McNemar test statistic with Yates' continuity correction
mcnemar_statistic = (abs(b - c) - 1)**2 / (b + c)
# Print the calculated statistic
print("McNemar's statistic:", round(mcnemar_statistic, 3))
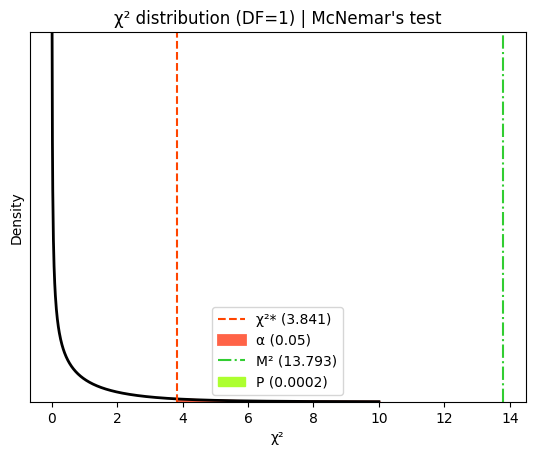
McNemar's statistic: 13.793
from scipy.stats import chi2
# Significance level (alpha)
α = 0.05
# Calculate critical chi-squared value
chi2_crit = chi2.ppf(1 - α, 1) # 1 degree of freedom
# Generate x values for plotting
x = np.linspace(0, 10, 1000) # Adjust range as needed
hx = chi2.pdf(x, 1) # Chi-squared PDF with 1 degree of freedom
# Create the plot
plt.plot(x, hx, lw=2, color="black")
# Plot the critical chi-squared value
plt.axvline(
x=chi2_crit, # type: ignore
color='orangered',
linestyle='--',
label=f"χ²* ({chi2_crit:.3f})")
# Shade the rejection region (alpha)
plt.fill_between(
x[x >= chi2_crit],
hx[x >= chi2_crit],
linestyle="-",
linewidth=2,
color='tomato',
label=f'α ({α})')
# Plot the observed chi-squared statistic
plt.axvline(
x=mcnemar_statistic,
color='limegreen',
linestyle='-.',
label=f"M² ({mcnemar_statistic:.3f})")
# Shade the P-value area
plt.fill_between(
x[x >= mcnemar_statistic],
hx[x >= mcnemar_statistic],
color='greenyellow',
label=f'P ({1 - chi2.cdf(mcnemar_statistic, 1):.4f})' # Calculate P value
)
# Add labels and title
plt.xlabel('χ²')
plt.ylabel('Density')
plt.margins(x=0.05, y=0)
plt.yticks([])
plt.title(f"χ² distribution (DF=1) | McNemar's test")
plt.legend();
We can easily conduct McNemar’s test using either the free web calculator available in the QuickCalcs section of graphpad.com or by utilizing the statsmodels library in Python.
from statsmodels.stats.contingency_tables import mcnemar
print(mcnemar(
table,
exact=False, # exact=False uses the chi-square distribution instead of binomial distribution
correction=True))
pvalue 0.00020408400998040742
statistic 13.793103448275861
In this specific case, the χ² value is 13.79 with one degree of freedom. This results in a two-tailed P value of 0.0002. In simpler terms, if there was truly no link between the risk factor and the disease, the chance of observing an odds ratio this far from 1.0 (indicating no association) is merely 0.02 percent.
Instead of getting caught up in the complexities of the chi-square approximation and whether or not to apply Yates’ correction (and which version to use), it is suggested opting for the binomial test. This provides an exact result, eliminating the need for such approximations and corrections.
print(mcnemar(table, exact=True))
pvalue 0.00010371580719947815
statistic 4.0
Bayesian approach#
In contrast to frequentist statistics, which focuses on the probability of observing data given a fixed hypothesis (P values), the Bayesian approach calculates the probability of a hypothesis being true given the observed data. This is achieved by combining prior knowledge (represented by a prior distribution) with the likelihood of the data to obtain a posterior distribution, which reflects our updated belief about the hypothesis after observing the data.
We previously introduced the Bayesian approach in the chapter on confidence intervals, where we focused on estimating a single population mean. In the context of the paired t-test, a Bayesian approach would estimate the probability distribution of the true mean difference, allowing us to make statements like “There’s a 95% probability that the true mean difference lies between these two values.”
# Perform Bayesian estimation of the mean difference
bayes_result = stats.bayes_mvs(differences_fert, alpha=0.95)
# Extract and print the results
posterior_mean = bayes_result[0][0]
credible_interval = bayes_result[0][1]
print(f"Bayesian estimate of the mean difference: {posterior_mean:.3f}")
print(f"95% credible interval for the mean difference: \
[{credible_interval[0]:.3f}, {credible_interval[1]:.3f}]")
Bayesian estimate of the mean difference: 2.617
95% credible interval for the mean difference: [0.004, 5.229]
# In fact many more information can be accessed
bayes_result
(Mean(statistic=2.6166666666666667, minmax=(0.00389916480019048, 5.2294341685331425)),
Variance(statistic=25.969965277777774, minmax=(11.931551867861122, 55.36591719484016)),
Std_dev(statistic=4.991122961308315, minmax=(3.45420784954541, 7.440827722427134)))
While this brief introduction provides a glimpse into the Bayesian perspective on paired t-tests, it’s important to recognize that Bayesian statistics is a vast and nuanced field. The choice of prior distributions, model selection, and computational techniques can significantly influence the results and interpretation of Bayesian analyses. Delving deeper into the intricacies of Bayesian inference would require a dedicated text, beyond the scope of this introductory chapter. However, for those intrigued by the potential of Bayesian methods, we encourage further exploration of this powerful statistical framework.
Non-parametric approach#
In the previous chapter on unpaired t-tests, we explored both parametric and non-parametric methods for comparing the means of two independent groups. We noted that parametric tests, like the t-test and ANOVA, are robust to minor deviations from normality, especially with large samples. However, when the assumptions of normality are violated, non-parametric methods offer valuable alternatives. These methods typically analyze the ranks of the data, making them less sensitive to outliers and deviations from normality. However, it’s important to remember that non-parametric tests might have lower statistical power compared to parametric tests when the data is truly Gaussian.
As a reminder, the follwoing flowchart was designed to help choosing between Pingouin’s functions adequate for a non-parametric analysis:
Performing the Wilcoxon signed-rand test manually#
Exact test#
The Wilcoxon matched-pairs signed-rank test assesses the null hypothesis that two related paired samples come from the same distribution. It specifically tests whether the distribution of the differences (x - y) is symmetric about zero. In simpler terms, it checks if the differences between matched pairs are equally likely to be positive or negative. Its underlying principle is to consider both the magnitude and direction of the differences between paired observations:
where \(x_i = (x_{1,i}, x_{2,i})\) represents the \(i\)-th pair of measurements, and \(R_i\) is the rank of the absolute difference \(|x_{2,i} - x_{1,i}|\).
The test works as follows:
Calculate the difference between each matched pair (e.g., ‘after - before’ or ‘treatment - control’) and note the sign of the difference, e.g., negative values refer to a decrease
Rank the absolute values of the differences, temporarily ignoring whether they are positive or negative
Sum the ranks of the positive differences and the ranks of the negative differences separately
Compute the test statistic W as the minimum between the two sums of ranks obtained in the previous step
Compute the P value: it represents the probability of observing a test statistic (in this case, the difference between the sums of ranks) as extreme as, or more extreme than, the one calculated from the data, assuming the null hypothesis is true. However, the specific way to compute this P value depends on the sample size and whether we’re using tables, the normal approximation, or exact methods, as discussed in the previous chapter for the Mann-Whitney U test
Pairs with large absolute differences have higher ranks, contributing more to W, while pairs with small differences have less influence. By focusing on ranks, the test is less sensitive to outliers and primarily detects shifts in median values between the two groups.
from scipy.stats import rankdata
# Make an array copy of the differences_fert Series
differences_array = differences_fert.to_numpy()
# Extract the signs of the differences
signs = np.sign(differences_array) # 1 for positive, -1 for negative, 0 for zero
# Print the differences and their signs
print("Differences:", differences_array)
print("Signs:", signs)
# Calculate ranks of absolute differences
ranks_abs_diff = rankdata(np.absolute(differences_array))
# Print the ranks with a descriptive message
print("Ranks of the absolute differences:", ranks_abs_diff, sep='\n')
Differences: [ 6.125 -8.375 1. 2. 0.75 2.875 3.5 5.125 1.75 3.625
7. 3. 9.375 7.5 -6. ]
Signs: [ 1. -1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. -1.]
Ranks of the absolute differences:
[11. 14. 2. 4. 1. 5. 7. 9. 3. 8. 12. 6. 15. 13. 10.]
It’s crucial to address two potential issues that can arise:
Ties: ties occur when two or more pairs have the same difference. The Wilcoxon test assigns the average rank to tied values. While this is a reasonable approach, a large number of ties can reduce the test’s expressiveness, making it less sensitive to subtle differences between the groups.
Zeros: zeros represent pairs with no difference between the measurements. These pairs don’t provide information about whether the distribution of differences is centered around zero, which is the null hypothesis of the test. Consequently, the Wilcoxon test typically discards pairs with zero differences. If a substantial proportion of pairs have zero differences, the test’s power can be significantly reduced.
# Calculate the sum of ranks for positive and negative differences
W_pos = np.sum(ranks_abs_diff[differences_fert > 0])
W_neg = np.sum(ranks_abs_diff[differences_fert < 0])
# Print the results with clear labels
print(f"Sum of ranks for positive differences (W+) = {W_pos}")
print(f"Sum of ranks for negative differences (W-) = {W_neg}")
# Compute the W-statistic as the minimum of W_pos and W_neg
W_statistic = min(W_pos, W_neg) # Corrected calculation
# Print the result
print(f"W-statistic: {W_statistic}")
Sum of ranks for positive differences (W+) = 96.0
Sum of ranks for negative differences (W-) = 24.0
W-statistic: 24.0
To determine the P value for the Wilcoxon signed-rank test, we can consult tables of critical values. These tables provide P values associated with different values of the test statistic W for various sample sizes. Most tables offer both one-sided and two-sided P values. If only one-sided P values are available, we can double them to obtain the two-sided P value.
The critical value is the threshold that W must exceed to reject the null hypothesis at a given significance level (α). If the calculated W statistic is slightly lower than the critical value W*, the P value should be approximately equal to the chosen alpha, e.g., P ≈ 0.05.
# Print the critical value and the calculated W-statistic
W_critical = 25
print(f"Critical W = {W_critical} for alpha = 0.05 and n = {len(differences_fert)}")
print(f"Calculated W-statistic = {W_statistic}")
# Compare the W-statistic to the critical value and draw a conclusion
if W_statistic <= W_critical:
print("Reject the null hypothesis. There is a significant difference between the groups.")
else:
print("Fail to reject the null hypothesis. There is no significant difference between the groups.")
Critical W = 25 for alpha = 0.05 and n = 15
Calculated W-statistic = 24.0
Reject the null hypothesis. There is a significant difference between the groups.
Calculating the exact null distribution for the Wilcoxon signed-rank test involves more intricate combinatorial calculations compared to the Mann-Whitney U test discussed previously. While we won’t delve into the specific details here, it’s important to be aware of the computational challenges involved, especially for larger sample sizes.
Asymptotic approach#
When both sample sizes are 10 or greater, we can approximate the distribution of W as a normal distribution with mean \(\mu_A\) and standard deviation \(\sigma_A\). This normal approximation simplifies the calculation of P values and is often used in statistical software.
from scipy.stats import norm
n = differences_fert_stats.nobs
# Significance level (alpha)
α = 0.05
# Determine the mean and standard deviation for the normal approximation
μ = n * (n + 1) / 4
σ = np.sqrt(n * (n + 1) * (2 * n + 1) / 24)
# Generate x values for plotting the normal distribution
x = np.linspace(μ - 4 * σ , μ + 4 * σ , 1000)
normal_pdf = norm.pdf(x, loc=μ, scale=σ )
# Create the plot
plt.plot(x, normal_pdf, lw=2, color="black")
# Plot the critical W-values (two-tailed test)
W_crit_lower = μ - norm.ppf(1 - α/2) * σ # Lower critical W
W_crit_upper = μ + norm.ppf(1 - α/2) * σ # Upper critical W
plt.axvline(
x=W_crit_lower,
color='orangered',
linestyle='--')
plt.axvline(
x=W_crit_upper,
color='orangered',
linestyle='--',
label=f"W* ({W_crit_lower:.3f})"
)
# Shade the rejection regions (alpha)
plt.fill_between(
x,
normal_pdf,
where=(x <= W_crit_lower) | (x >= W_crit_upper),
linestyle="-",
linewidth=2,
color='tomato',
label=f"α ({α})"
)
# Calculate the z-score
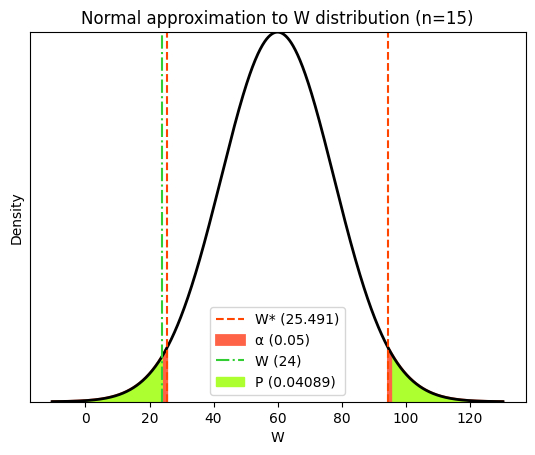
W_crit = (W_statistic - μ) / σ
# Calculate the p-value (two-tailed)
p_value_W = 2 * (1 - norm.cdf(abs(W_crit)))
# Plot the observed W-statistic
plt.axvline(
x=float(W_statistic),
color='limegreen',
linestyle='-.',
label=f"W ({W_statistic:n})"
)
# Shade the P-value areas (two-tailed)
plt.fill_between(
x,
normal_pdf,
where=(x <= W_statistic) | (x >= μ + (μ - W_statistic)),
color='greenyellow',
label=f"P ({p_value_W:.5f})"
)
# Add labels and title
plt.xlabel('W')
plt.ylabel('Density')
plt.margins(x=0.05, y=0)
plt.yticks([])
plt.title(f"Normal approximation to W distribution (n={n})")
plt.legend();
Python tools for the non-parametric paired t-test#
Python offers convenient tools for running the Wilcoxon signed-rank test, simplifying analysis and providing additional functionalities.
SciPy provides a comprehensive collection of statistical functions, including the wilcoxon function for performing the Wilcoxon signed-rank test.
from scipy.stats import wilcoxon
# Perform Wilcoxon signed-rank test with exact p-value calculation
W_statistic_exact, p_value_exact = wilcoxon(differences_fert, method='exact')
# Perform Wilcoxon signed-rank test with normal approximation p-value calculation
W_statistic_asymptotic, p_value_asymptotic = wilcoxon(differences_fert, method='approx', correction=False)
# Print the results
print("Wilcoxon signed-rank test results:")
print(f" Exact P value: {p_value_exact:.5f}")
print(f" Asymptotic P value (similar to normal distribution method): {p_value_asymptotic:.5f}")
Wilcoxon signed-rank test results:
Exact P value: 0.04126
Asymptotic P value (similar to normal distribution method): 0.04089
While SciPy provides the core functionality for the Mann-Whitney U test, Pingouin offers a more streamlined function wilcoxon with additional features.
# Perform Wilcoxon signed-rank test using Pingouin
pg.wilcoxon(
differences_fert,
method='approx',
correction=False, # Pingouin applies a continuity correction by default
)
| W-val | alternative | p-val | RBC | CLES | |
|---|---|---|---|---|---|
| Wilcoxon | 24.0 | two-sided | 0.040888 | 0.6 | NaN |
When the P value is less than 0.05 in a two-tailed Wilcoxon signed-rank test, we generally conclude that there is a significant difference between the paired groups being compared. However, in our case, the P value is borderline, as seen with the parametric tests. The calculated W (24) is slightly lower than the critical value (25), suggesting that the P value is close to the significance level of 0.05. While we still reject the null hypothesis, it’s important to acknowledge the borderline nature of this result and consider the possibility of a type I error (false positive).
Bootstrapping and permutation tests for paired data#
Bootstrapping offers a robust alternative for statistical inference, particularly useful when dealing with small sample sizes or when the assumptions of traditional parametric tests might not be fully met. Bootstrapping allows us to estimate parameters and confidence intervals directly from the data itself, without relying on strong assumptions about the underlying population distribution. This approach, known as non-parametric inference, was previously encountered in the chapter on calculating the confidence interval of a mean (univariate), as well as in the chapter on comparing two means with unpaired t test.
While bootstrapping is primarily used for estimation, permutation tests, another resampling-based method, are specifically designed for hypothesis testing. They can be employed to test various hypotheses, such as the null hypothesis of exchangeability (where group labels are irrelevant) or the hypothesis of equal means after shifting the group means to a common value.
Recent research has explored the application of bootstrap and permutation methods to paired data, particularly when the distributions of the paired differences might deviate from normality. A study by Konietschke and Pauly (2014) demonstrated that even when the data may not be perfectly exchangeable under the null hypothesis, certain permutation and bootstrap approaches can provide valid and powerful alternatives to the traditional t-test. These methods, which may involve resampling or permuting the data while accounting for the dependency structure within pairs, have been shown to improve the power of the test under conditions of non-normality. This highlights the potential of bootstrap and permutation methods to provide more robust and reliable inferences in situations where the assumptions of the paired t-test might be violated.
Generating bootstrap pair samples#
The core idea behind bootstrapping remains the same as for unpaired observations: treat our observed sample as a miniature representation of the population. However, in the context of paired data, we resample the pairs of observations, preserving the crucial relationship between the two measurements within each pair. We repeatedly resample (with replacement) from our original set of pairs to create multiple bootstrap samples. Each replicate is a new dataset of the same size, but now consisting of these resampled pairs.
For each bootstrap sample, we calculate the statistic of interest, i.e., in this case, the mean difference between the paired measurements. This generates a bootstrap distribution of paired differences mean, which serves as an approximation of how this statistic would vary if we were to repeatedly sample pairs from the population.
# Set random seed for reproducibility
np.random.seed(111)
# Generate 10000 bootstrap replicates of the mean difference
n_replicates = 10000
bs_differences_means = np.array([
np.mean(
np.random.choice(
differences_fert,
size=len(differences_fert),
replace=True
)) for _ in range(n_replicates)
])
print(bs_differences_means[:6]) # print the 6 first replicates
[3.41666667 3.40833333 3.375 0.775 1.80833333 3.65 ]
Estimate of the confidence interval for the paired difference mean#
Once we have the bootstrap distribution of the paired difference means, we can estimate the confidence interval by finding the percentiles corresponding to the desired confidence level.
For a 95% confidence interval, we typically use the 2.5th and 97.5th percentiles of the bootstrap distribution of the difference means. This means that 95% of the bootstrap estimates of the paired difference mean fall within this interval, providing a range of plausible values for the true population mean difference.
# Calculate the 95% CI and the standard error
bs_m = np.mean(bs_differences_means)
bs_CI = np.round(np.percentile(bs_differences_means, [2.5, 97.5]), 2)
bs_s = np.std(bs_differences_means, ddof=1)
# Print the results
print(f"Bootstrap estimate of the mean of the paired differences= {bs_m:5.2f}")
print(f"95% bootstrap percentile CI = {bs_CI}")
print(f"Bootstrap standard error = {bs_s:.5f}")
Bootstrap estimate of the mean of the paired differences= 2.63
95% bootstrap percentile CI = [0.16 4.76]
Bootstrap standard error = 1.17700
It’s generally expected that the confidence interval obtained through bootstrapping, here [0.16, 4.76], will be reasonably similar to the confidence interval calculated using the t-distribution (here [0.004, 5.229]), especially when the sample size is sufficiently large and the underlying assumptions of the paired t-test are met.
Interestingly, in this case, the confidence interval obtained through bootstrapping is narrower than the one derived from the t-distribution. This might seem counterintuitive, as we generally expect wider confidence intervals with smaller sample sizes due to increased uncertainty. However, bootstrapping can be less sensitive to violations of the normality assumption (which the paired t-test relies on), potentially leading to a narrower interval when the distribution of the paired differences deviates from normality.
# Plot the histogram of the bootstrap distribution of mean paired differences
plt.hist(
bs_differences_means,
density=False,
bins='auto',
color='gold',
label='Bootstrap mean difference')
# Annotate the observed mean difference
plt.axvline(
x=differences_fert_stats.mean, # type: ignore
color='cornflowerblue',
linestyle='-', lw=2,
label=f'Observed mean difference ({differences_fert_stats.mean:.3f})')
# Add lines for the confidence interval
plt.axvline(
x=bs_CI[0],
color='red',
linestyle='--',
label=f'2.5th ({bs_CI[0]:.2f})')
plt.axvline(
x=bs_CI[1],
color='red',
linestyle='--',
label=f'97.5th ({bs_CI[1]:.2f})')
# Add labels and title
plt.xlabel('Mean difference')
plt.ylabel('Frequency')
plt.title(f"Bootstrap distribution of the mean difference (B={n_replicates})")
plt.legend();
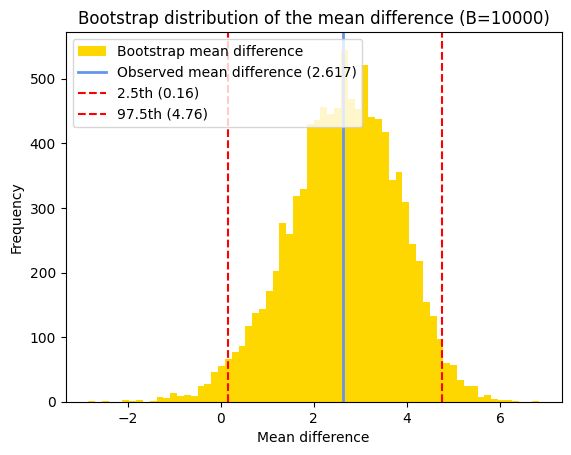
Given the symmetrical distribution of our bootstrapped mean paired differences, we can also estimate the confidence interval using the normal approximation and the previously calculated bootstrap standard error.
# Calculate the 95% normal margin of error
z_crit = norm.ppf(0.975)
bs_w = z_crit * bs_s
# Calculate confidence interval
bs_ci_normal = np.round((bs_m - bs_w, bs_m + bs_w), 5)
# Print the result
print(f"95% normal percentile CI of bootstrap distribution = {bs_ci_normal}")
95% normal percentile CI of bootstrap distribution = [0.3267 4.94045]
Bootstrapping with Pingouin#
The compute_bootci method from the pingouin library proves to be a valuable asset in such scenarios, as it streamlines the process of generating confidence intervals using bootstrapping. It eliminates the need for manual creation of bootstrap samples, offering a variety of methods for confidence interval computation, including the normal approximation, percentile bootstrap, and bias-corrected percentile method. Additionally, it provides the flexibility to return the entire bootstrap distribution, enabling further exploration and visualization of the resampling results.
import pingouin as pg
# Calculate 95% percentile bootstrap confidence interval using pingouin
bs_ci, bt = pg.compute_bootci(
x=differences_fert, # Use the array of paired differences
func=np.mean, # Calculate the mean of each bootstrap sample
confidence=0.95,
method='per',
seed=1234,
decimals=3,
n_boot=10000,
return_dist=True)
print(bt[:10]) # Print the first 10 bootstrap replicate means
print(
f"95% percentile bootstrap confidence interval (pingouin): ({bs_ci[0]:.3f}, {bs_ci[1]:.3f})")
[1.525 0.53333333 4.33333333 1.19166667 1.76666667 3.875
3.075 3.35 1.75833333 2.01666667]
95% percentile bootstrap confidence interval (pingouin): (0.192, 4.750)
Bootstrap P value for paired data#
Similar to the unpaired t-test, bootstrapping and permutation tests offer flexibility in hypothesis testing for paired data as well. We can employ resampling techniques to generate data under the null hypothesis, allowing us to compute P values. The key lies in choosing a relevant test statistic and calculating it consistently for both the original and resampled data.
In the context of a paired t-test, the t-statistic and the mean (paired) difference serve as natural and straightforward test statistics. However, we can also explore other statistics like the median difference or even specific quantile differences if the research question demands it.
Bootstrapped t-statistics of shifted differences#
We can adapt Bradley Efron’s bootstrapping algorithm for the paired t-test scenario. The core idea remains the same: shift the data to simulate the null hypothesis. However, instead of shifting individual groups, we shift the differences within each pair to have a common mean of zero (representing no difference under the null hypothesis).
Specifically, we create a new dataset of shifted differences as \(d_i' = d_i - \bar d\), where \(d_i\) are the original paired differences and \(\bar d\) is their mean.
Next, we perform the following steps B times (e.g., B = 10000):
Draw a bootstrap sample \(d_i^b\) of size \(n\) with replacement from the shifted differences \(d_i'\).
Calculate the t-statistic \(T^b_i\) using the bootstrap sample \(d_i^b\).
One-tailed P value#
To estimate the P value using bootstrapping, we assess how often the bootstrapped t-statistics (\(T^b_i\)) are as extreme as, or more extreme than, the observed t-statistic (\(t\)) from the original data. This involves generating multiple bootstrap samples, calculating the t-statistic for each, and determining the proportion of these bootstrap t-statistics that exceed the observed t-statistic.
Mathematically, the bootstrap p-value (\(p_B\)) can be expressed as:
However, when testing a directional hypothesis (one-tailed test), we need to consider the direction of the effect. If the alternative hypothesis states that the true value is less than the hypothesized value, and the observed test statistic is negative (\(t < 0\)), the p-value is calculated as:
where \(I\{\text{condition}\} = 1\) if the condition is true and \(0\) otherwise.
Conversely, if the alternative hypothesis states that the true value is greater than the hypothesized value, and the observed test statistic is positive (\(t > 0\)), the p-value is calculated as:
While adding 1 to both the numerator and denominator of the p-value calculation is sometimes suggested to avoid a p-value of 0, this practice is not universally accepted.
And as discussed in the previous chapter, there are several approaches to calculate a two-tailed P value from a bootstrap distribution. These range from conservative methods that multiply the highest one-tailed P value by 2 to more flexible methods that sum the probabilities in both tails. Additionally, while the “99 rule” suggests that 99 replicates may be sufficient for estimating confidence intervals, particularly for the median, we’ll generally use a higher number of replicates (B = 9999) in our analyses to ensure greater precision.
# Set the random seed for reproducibility
np.random.seed(111)
n_replicates = 10**4 - 1 # 99 rule
# Shift the paired differences to have a mean of zero (simulating the null hypothesis)
shifted_differences = differences_fert - differences_fert_stats.mean # type: ignore
# Generate 10000 bootstrap replicates of the shifted differences
bs_shifted_diffs = np.array([
np.random.choice(shifted_differences, size=differences_fert_stats.nobs, replace=True)
for _ in range(n_replicates)
])
# Calculate the mean and standard deviation for each bootstrap replicate
bs_shifted_diffs_means = np.mean(bs_shifted_diffs, axis=1)
bs_shifted_diffs_stds = np.std(bs_shifted_diffs, ddof=1, axis=1) # Sample standard deviation
# Calculate the standard error for each replicate
bs_se = bs_shifted_diffs_stds / differences_fert_stats.nobs**.5
# Calculate the t-statistic for each bootstrap replicate
bs_t_statistic = bs_shifted_diffs_means / bs_se
# Or we calculate the t-test for the mean on the one-sample bootstrap distribution
# bs_t_statistic = np.array([
# stats.ttest_1samp(sample, popmean=0)[0] for sample in bs_shifted_diffs
# ])
# Print the first 15 t-statistics from the bootstrap replicates
print(bs_t_statistic[:15])
[ 1.08228839 0.5891132 0.83625618 -1.43918435 -0.55298715 0.92978128
0.140706 1.14955388 0.29781496 -0.73463324 2.46303042 -0.24038272
0.75223906 0.58088937 -0.39851653]
# Calculate the P value using bootstrapping, considering the direction of the observed t-statistic
# # 1. Calculate lower and upper tail
if t_statistic_paired >= 0:
# p_value_bs_shifted_low = np.sum(bs_t_statistic_welch >= t_statistic_welch) / len(bs_t_statistic_welch)
p_value_bs_shifted_up = np.mean(bs_t_statistic >= t_statistic_paired) # Mathematically same as above
p_value_bs_shifted_low = np.mean(bs_t_statistic <= -t_statistic_paired)
else:
p_value_bs_shifted_low = np.mean(bs_t_statistic <= t_statistic_paired)
p_value_bs_shifted_up = np.mean(bs_t_statistic >= -t_statistic_paired)
# 2. Attribute the one-tailed P value
p_value_bs_shifted_1t = p_value_bs_shifted_up if t_statistic_paired >= 0 else p_value_bs_shifted_low
# Print the P value
print(f"One-sided P value obtained using bootstrapped paired-sample t-statistics = {p_value_bs_shifted_1t:.4f}")
One-sided P value obtained using bootstrapped paired-sample t-statistics = 0.0681
import matplotlib.patches as mpatches
# Plot the histogram of the bootstrap t-statistics
hist, bins, patches = plt.hist(
bs_t_statistic,
density=False,
bins=int(n_replicates**.5),
color='gold',
)
# Annotate the observed t-statistic
plt.axvline(
x=t_statistic_paired,
color='limegreen',
linestyle='-.', lw=2,
label=f'Observed t ({t_statistic_paired:.3f})')
# Determine the direction of the observed t-statistic and plot accordingly
if t_statistic_paired >= 0:
# Plot the histogram of the bootstrap t-statistics >= observed t-statistic
extreme_t_stats = bs_t_statistic[bs_t_statistic >= t_statistic_paired]
# Change the color of the bars based on the direction parameter
for i, bin_edge in enumerate(bins[:-1]):
if np.any(bin_edge >= extreme_t_stats):
patches[i].set_facecolor('lime') # type: ignore
else:
# Plot the histogram of the bootstrap t-statistics <= observed t-statistic
extreme_t_stats = bs_t_statistic[bs_t_statistic <= t_statistic_paired]
for i, bin_edge in enumerate(bins[:-1]):
if np.any(bin_edge <= extreme_t_stats):
patches[i].set_facecolor('lime') # type: ignore
# Add labels and title
plt.xlabel(r'$t$')
plt.ylabel('Frequency')
plt.title(f"Bootstrap distribution of t under H0 (B={n_replicates})")
# Create a copy of the original patch for the legend
original_patch = mpatches.Patch(color='gold', label='Bootstrap t')
# Create a patch for the legend
p_value_patch = mpatches.Patch(color='lime', label=f'One-tailed P ({p_value_bs_shifted_1t:.3f})')
# Add the patches to the legend
plt.legend(handles=[original_patch, plt.gca().lines[0], p_value_patch]); # type: ignore
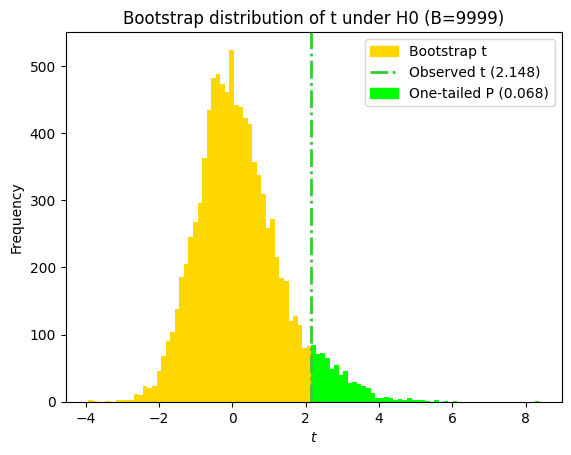
# Maximum one-tail
p_value_bs_shifted_2t_max = 2 * max(p_value_bs_shifted_low, p_value_bs_shifted_up)
# Sum of the tails
p_value_bs_shifted_2t_sum = p_value_bs_shifted_low + p_value_bs_shifted_up
# Print the results
print(f"Two-tailed paired-sample t-test bootstrap P value (conservative) = {p_value_bs_shifted_2t_max:.4f}")
print(f"Two-tailed paired-sample t-test bootstrap P value (both tails) = {p_value_bs_shifted_2t_sum:.4f}")
Two-tailed paired-sample t-test bootstrap P value (conservative) = 0.1362
Two-tailed paired-sample t-test bootstrap P value (both tails) = 0.0770
Since the distribution of the bootstrapped t-statistic obtained with paired mean differences isn’t perfectly symmetrical, it’s more accurate to calculate the two-tailed P value by summing the probabilities in both tails, even though the resulting P value is already greater than the significance level (alpha). This approach avoids relying on the symmetry assumption and provides a more robust estimate of the P value.
P value via permutation#
When conducting a paired t-test, permutation tests are often the preferred resampling method for creating data that would be expected if the null hypothesis were true. In this approach, we randomly flip the sign of each difference within a pair (changing X-Y to Y-X). This shuffling maintains the variation between different pairs, but it only keeps the original pattern of differences within each pair if the true average difference is actually zero (as the null hypothesis states).
def permute_paired_differences(differences):
"""
Generates a permuted sample of paired differences under the null hypothesis.
Args:
differences: An array of paired differences.
Returns:
A new array with randomly negated differences within each pair.
"""
# Randomly generate -1 or 1 for each pair
signs = np.random.choice([-1, 1], size=len(differences))
# Multiply each difference by its corresponding sign
permuted_differences = differences * signs
return permuted_differences
Next, we determine how frequently these permuted differences are as extreme as, or even more extreme than, the observed mean difference in our original data. This proportion represents the P value. In essence, it tells us the likelihood of observing a difference as large (or larger) as the one we found, purely by chance, if there were truly no difference between the groups (i.e., if the null hypothesis were true).
# Set random seed for reproducibility
np.random.seed(111)
# Generate 10,000 bootstrap replicates of the mean difference for each permutation sample
n_replicates = 10**4 - 1
# Initialize an empty array to store the permuted mean differences
permuted_diffs_means = np.zeros(n_replicates)
# Generate permuted mean differences
for i in range(n_replicates):
# Permute the differences
permuted_diffs = permute_paired_differences(differences_fert)
# Calculate the mean difference for this permuted sample
permuted_diffs_means[i] = np.mean(permuted_diffs)
# Generate permuted mean differences using a list comprehension
# permuted_diffs_means = np.array(
# [np.mean(permute_paired_differences(differences_fert)) for _ in range(n_replicates)])
# Print the first 6 replicate difference means
print(permuted_diffs_means[:6])
[ 0.88333333 -2.11666667 -0.1 0.78333333 -0.95 -2.03333333]
# Calculate the P value using bootstrapping, considering the direction of the observed paired difference mean
if differences_fert_stats.mean >= 0:
p_value_permutation_up = np.mean(permuted_diffs_means >= differences_fert_stats.mean)
p_value_permutation_low = np.mean(permuted_diffs_means <= -differences_fert_stats.mean)
else:
p_value_permutation_low = np.mean(permuted_diffs_means <= differences_fert_stats.mean)
p_value_permutation_up = np.mean(permuted_diffs_means >= -differences_fert_stats.mean)
p_value_permutation_1t = p_value_permutation_up if differences_fert_stats.mean >= 0 else p_value_permutation_low
# Print the P value
print(f"One-sided P value obtained using permutation test (mean difference) = {p_value_permutation_1t:.4f}")
One-sided P value obtained using permutation test (mean difference) = 0.0264
# Plot the histogram of the permuted mean differences
hist, bins, patches = plt.hist(
permuted_diffs_means,
density=False,
bins=int(n_replicates**.5),
color='gold',
)
# Annotate the observed mean difference
plt.axvline(
x=differences_fert_stats.mean, # type: ignore
color='limegreen',
linestyle='-.', lw=2,
label=f'Observed mean difference ({differences_fert_stats.mean:.3f})')
# Determine the direction of the observed mean difference and plot accordingly
if differences_fert_stats.mean >= 0:
# Plot the histogram of the mean differences >= observed mean difference
extreme_diffs = permuted_diffs_means[permuted_diffs_means >= differences_fert_stats.mean]
# Change the color of the bars based on the direction parameter
for i, bin_edge in enumerate(bins[:-1]):
if np.any(bin_edge >= extreme_diffs):
patches[i].set_facecolor('lime') # type: ignore
else:
# Plot the histogram of the mean differences <= observed mean difference
extreme_diffs = permuted_diffs_means[permuted_diffs_means <= differences_fert_stats.mean]
for i, bin_edge in enumerate(bins[:-1]):
if np.any(bin_edge <= extreme_diffs):
patches[i].set_facecolor('lime') # type: ignore
# Add labels and title
plt.xlabel('Mean difference')
plt.ylabel('Frequency')
plt.title(f"Distribution of bootstrap mean differences under H0 (B={n_replicates})")
# Create a copy of the original patch for the legend
original_patch = mpatches.Patch(color='gold', label='Bootstrap mean difference')
# Create a patch for the legend
p_value_patch = mpatches.Patch(color='lime', label=f'One-tailed P ({p_value_permutation_1t:.3f})')
# Add the patches to the legend
plt.legend(handles=[original_patch, plt.gca().lines[0], p_value_patch]); # type: ignore
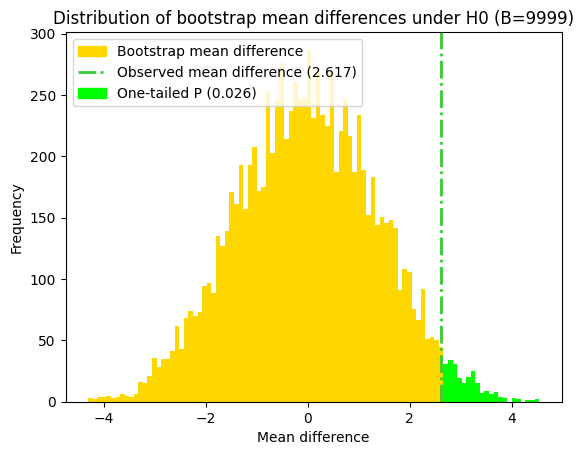
# Maximum one-tail
p_value_permut_2t_max = 2 * max(p_value_permutation_low, p_value_permutation_up)
# Sum of the tails
p_value_permut_2t_sum = p_value_permutation_low + p_value_permutation_up
# Print the results
print(f"Two-tailed permutation bootstrap P value (conservative) = {p_value_permut_2t_max:.4f}")
print(f"Two-tailed permutation bootstrap P value (both tails) = {p_value_permut_2t_sum:.4f}")
Two-tailed permutation bootstrap P value (conservative) = 0.0546
Two-tailed permutation bootstrap P value (both tails) = 0.0537
Our analysis of the paired data yielded mixed results regarding the significance of the observed difference between the groups. The frequentist paired t-test produced a borderline P value of 0.0497, suggesting a statistically significant difference at the conventional alpha level of 0.05. The non-parametric Wilcoxon signed-rank test, using both exact and asymptotic methods, also yielded borderline P values (0.04126 and 0.04089, respectively).
However, the bootstrap analysis with shifted differences resulted in a non-significant two-sided P value of 0.0770. This discrepancy might stem from the sensitivity of bootstrapping to small sample sizes, which can introduce variability in the results.
The permutation test provided the strongest evidence for a statistically significant difference, with a P value of 0.0537. While the frequentist test also hinted at a potential effect, it was less conclusive.
Given the borderline significance and the potential limitations of bootstrapping with small samples, interpreting these findings requires caution. Further investigation with a larger sample size or additional analyses might be necessary to confirm the presence of a true effect.
Conclusion#
This chapter has provided a comprehensive guide to the paired t-test, a powerful statistical method for analyzing differences between paired observations. We began by establishing the foundations of the test, emphasizing its focus on assessing changes within matched pairs or repeated measurements. We then explored the crucial steps involved in preparing data for hypothesis testing, including descriptive statistics, visualization techniques, and assessing the normality assumption.
The core of the chapter delved into the mechanics of the paired t-test, explaining the t-ratio, its manual calculation, and its interpretation in terms of P values and confidence intervals. We demonstrated how to leverage Python libraries like scipy.stats and pingouin to streamline the analysis process and gain deeper insights from the results.
Furthermore, we extended our exploration to encompass variations and extensions of the paired t-test, including one-sided tests for directional hypotheses, ratio paired t-tests for analyzing proportional changes, the McNemar test for paired categorical data, and a brief introduction to the Bayesian approach for estimating the probability distribution of the mean difference.
Finally, we touched upon the potential of bootstrap and permutation methods to provide robust alternatives to the paired t-test, particularly when dealing with non-normal data or violations of the test’s assumptions.
By combining theoretical understanding with practical implementation and a consideration of various extensions and alternatives, this chapter has equipped you with the knowledge and tools to confidently apply the paired t-test in your own research endeavors. Remember that careful consideration of the research question, data characteristics, and appropriate statistical techniques is crucial for drawing meaningful and valid conclusions from paired data.
Cheat sheet#
Descriptive statistics and visualization#
differences = x - y
# Concatenate the data in a DataFrame for some operations
data_diffs = pd.concat(
[x, y],
keys=['x', 'y'],
axis=1)
# Descriptive statistics
import scipy.stats as stats
stats.describe(differences)
# Boxplots
import matplotlib.pyplot as plt
import seaborn as sns
sns.stripplot(y=differences)
sns.boxplot(y=differences,)
# Before-after plots
import pingouin as pg
pg.plot_paired(
# We need to reshape the DataFrame in the long format
data=differences.reset_index().melt(
value_vars=['x', 'y'],
id_vars='index',
var_name='variable',
value_name='value'),
dv='value',
within='variable',
subject='index',)
Assessing assumptions#
Normality testing#
# Using scipy.stats
# D'Agostino-Pearson K² test
stats.normaltest(differences)
# Shapiro-Wilk
stats.shapiro(differences)
# Using pingouin
pg.normality(differences, method='normaltest')
pg.normality(differences, method='normaltest')
Q-Q plot#
pg.qqplot(differences, dist='norm', confidence=0.95)
T-test#
# Using scipy.stats
stats.ttest_rel(x, y)
# t = stats.ttest_rel(x, y)[0]
# Using pingouin
pg.ttest(x=x, y=y, paired=True)
# One-sided t-test
pg.ttest(x, y, paired=True, alternative='greater')
# Ratio paired t-test
# Perform the paired t-test on the log-transformed data
pg.ttest(
np.log10(x),
np.log10(y),
paired=True,)
# McNemar's test
from statsmodels.stats.contingency_tables import mcnemar
print(mcnemar(table, exact=False, correction=True))
# Bayesian estimation
table = np.array([[a, b], [c, d]])
stats.bayes_mvs(differences, alpha=0.95)
# Effect size (Cohen's d)
# Calculate unbiased Cohen's d using pingouin
pg.compute_effsize(x, y, paired=True, eftype='Cohen')
Non-parametric Wilcoxon signed-rank test#
from scipy.stats import wilcoxon
# Perform Wilcoxon signed-rank test with exact p-value calculation
wilcoxon(differences, method='exact')
# Perform Wilcoxon signed-rank test with normal approximation p-value calculation
wilcoxon(differences, method='approx', correction=False)
# Perform Wilcoxon signed-rank test using Pingouin
pg.wilcoxon(
differences,
method='approx',
correction=False, # Pingouin applies a continuity correction by default
)
Bootstrapping and permutation tests#
Bootstrap pair samples#
# Generate B bootstrap replicates of the mean difference, with replacement
n_replicates = 10000
differences_means = np.array([
np.mean(
np.random.choice(
differences,
size=len(differences),
replace=True
)) for _ in range(n_replicates)
])
# Calculate the statistics of interest `bs` for each replicate
bs_m = np.mean(differences_means)
bs_s = np.std(differences_means, ddof=1)
# Confidence interval
np.percentile(differences_means, [2.5, 97.5])
# 95% normal confidence interval
bs_w = norm.ppf(0.975) * bs_s
(bs_m - bs_w, bs_m + bs_w)
# Bootstrapping with Pingouin
bs_ci, bt = pg.compute_bootci(x=differences, func=np.mean, return_dist=True)
P value#
Bootstrapped t-statistics of shifted differences#
n_replicates = 10**4 - 1 # 99 rule
# Shift the paired differences to have a mean of zero (simulating the null hypothesis)
shifted_differences = differences - np.mean(differences)
# Generate B bootstrap replicates of the shifted differences
bs_shifted_diffs = np.array([
np.random.choice(shifted_differences, size=len(differences), replace=True)
for _ in range(n_replicates)
])
# Calculate the t-statistic for each bootstrap replicate
bs_shifted_diffs_means = np.mean(bs_shifted_diffs, axis=1) # mean
bs_shifted_diffs_stds = np.std(bs_shifted_diffs, ddof=1, axis=1) # std
bs_se = bs_shifted_diffs_stds / np.sqrt(len(differences)) # se
bs_t = bs_shifted_diffs_means / bs_se
# Calculate P values using bootstrapping, considering the direction of the observed statistic
# 1. Calculate lower and upper tail
if t >= 0:
p_value_bs_t_up = np.mean(bs_t >= t)
p_value_bs_t_low = np.mean(bs_t <= -t)
else:
p_value_bs_t_low = np.mean(bs_t <= t)
p_value_bs_t_up = np.mean(bs_t >= -t)
# 2. Attribute the one-tailed P value
p_value_bs_t_up if t >= 0 else p_value_bs_t_low
# 3. Attribute the two-tailed P values
# Maximum one-tail
2 * max(p_value_bs_t_low, p_value_bs_t_up)
# Sum of the tails
p_value_bs_t_low + p_value_bs_t_up
Permutation#
def permute_paired_differences(differences):
# Randomly generate -1 or 1 for each pair
signs = np.random.choice([-1, 1], size=len(differences))
# Multiply each difference by its corresponding sign
permuted_differences = differences * signs
return permuted_differences
permuted_diffs_means = np.array([
np.mean(permute_paired_differences(differences)) for _ in range(n_replicates)
])
# Calculate permutation P values
diff_mean = np.mean(differences)
if mean_diff >= 0:
p_value_permutation_up = np.mean(permuted_diffs_means >= diff_mean)
p_value_permutation_low = np.mean(permuted_diffs_means <= -diff_mean)
else:
p_value_permutation_low = np.mean(permuted_diffs_means <= diff_mean)
p_value_permutation_up = np.mean(permuted_diffs_means >= -diff_mean)
# One-tailed P value
p_value_permutation_up if diff_mean >= 0 else p_value_permutation_low
# Two-tailed P values
# Maximum one-tail
2 * max(p_value_permutation_low, p_value_permutation_up)
# Sum of the tails
p_value_permutation_low + p_value_permutation_up
Session information#
The output below details all packages and version necessary to reproduce the results in this report.
Show code cell source
!python --version
print("-------------")
from importlib.metadata import version
# List of packages we want to check the version
packages = ['numpy', 'pandas', 'matplotlib', 'seaborn', 'scipy', 'pingouin', 'statsmodels']
# Initialize an empty list to store the versions
versions = []
# Loop over the packages
for package in packages:
try:
# Get the version of the package
package_version = version(package)
# Append the version to the list
versions.append(package_version)
except Exception: # Use a more general exception for broader compatibility
versions.append('Not installed')
# Print the versions
for package, version in zip(packages, versions):
print(f'{package}: {version}')
Python 3.12.7
-------------
numpy: 1.26.4
pandas: 2.2.2
matplotlib: 3.9.2
seaborn: 0.13.2
scipy: 1.14.1
pingouin: 0.5.5
statsmodels: 0.14.2
